题目内容
 (1997•贵阳)如图,已知四边形BCDE是⊙O的内接四边形,又是⊙H的外切四边形,P、N、M、G为切点,BE、CD的延长线交于A点,若AP>BC,且AP,BC的长为方程x2-25x+150=0的两个根.求DE的长.
(1997•贵阳)如图,已知四边形BCDE是⊙O的内接四边形,又是⊙H的外切四边形,P、N、M、G为切点,BE、CD的延长线交于A点,若AP>BC,且AP,BC的长为方程x2-25x+150=0的两个根.求DE的长.分析:先求出方程的根,得出AP、BC的长,利用切线的性质分别得出△AED及△ABC的周长,判断出△ABC∽△ADE,继而可得
=
,代入即可得出DE的长度.
| △ABC的周长 |
| △ADE的周长 |
| BC |
| DE |
解答: 解:x2-25x+150=0,
解:x2-25x+150=0,
解得:x1=15,x2=10,
∵AP>BC,且AP,BC的长为方程x2-25x+150=0的两个根,
∴AP=15,BC=10,
∵⊙H与AB,BC,AC切于P、N、M点,
∴BN=BP,CN=CM,
∴BP+CM+BC=2BC=20,
∴△ABC的周长为50,
又∵EP,EG,DG,DM为⊙H的切线,
∴EP=EG,DG=DM,
∴AE+EG+GD+AD=2AP,
∴△AED的周长为30,
∵四边形BCDE是⊙O的内接四边形,
∴∠ADE=∠B,
又∵∠A=∠A,
∴△ABC∽△ADE,
∴
=
=
=
,
解得:DE=6.
答:DE的长为6.
 解:x2-25x+150=0,
解:x2-25x+150=0,解得:x1=15,x2=10,
∵AP>BC,且AP,BC的长为方程x2-25x+150=0的两个根,
∴AP=15,BC=10,
∵⊙H与AB,BC,AC切于P、N、M点,
∴BN=BP,CN=CM,
∴BP+CM+BC=2BC=20,
∴△ABC的周长为50,
又∵EP,EG,DG,DM为⊙H的切线,
∴EP=EG,DG=DM,
∴AE+EG+GD+AD=2AP,
∴△AED的周长为30,
∵四边形BCDE是⊙O的内接四边形,
∴∠ADE=∠B,
又∵∠A=∠A,
∴△ABC∽△ADE,
∴
| △ABC的周长 |
| △ADE的周长 |
| BC |
| DE |
| 10 |
| DE |
| 50 |
| 30 |
解得:DE=6.
答:DE的长为6.
点评:本题属于圆的综合题,涉及了切线的性质、相似三角形的判定与性质,综合性较强,注意掌握相似三角形的周长之比等于两三角形的相似比,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (1997•贵阳)如图,直线l经过A,B两点(A,B两点的坐标如图所示).求直线l所表示的一次函数的解析式.
(1997•贵阳)如图,直线l经过A,B两点(A,B两点的坐标如图所示).求直线l所表示的一次函数的解析式. (1997•贵阳)已知:如图,AC为⊙O的直径,BC为⊙O的切线,C为切点,且劣弧CN=弧CD,求证:
(1997•贵阳)已知:如图,AC为⊙O的直径,BC为⊙O的切线,C为切点,且劣弧CN=弧CD,求证: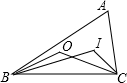 (1997•贵阳)已知:如图,I为△ABC的内心,O为△ABC的外心,∠O=140°,则∠I=( )
(1997•贵阳)已知:如图,I为△ABC的内心,O为△ABC的外心,∠O=140°,则∠I=( ) (1997•贵阳)某建筑基地横断面是梯形,如图,DC∥AB,梯形的高DE的长为5m,斜坡AD的坡度为I=
(1997•贵阳)某建筑基地横断面是梯形,如图,DC∥AB,梯形的高DE的长为5m,斜坡AD的坡度为I=