Question

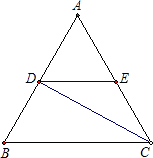如图，等边△ABC中，CD平分∠ACB，DE∥BC．
求证：DE=DB．

Answer 1

证明：∵△ABC是等边三角形，
∴∠ACB=∠B=60°，
∵CD平分∠ACB，
∴∠ACD=∠BCD，
∵DE∥BC，
∴∠EDC=∠DCB，
∴∠EDC=∠ECD，
∴DE=CE，
∵DE∥BC，
∴∠ADE=∠B，∠AED=∠ACB，
∴∠AED=∠ADE，
∴AE=AD，
∵AB=AC，
∴BD=CE，
∴DE=DB．
分析：根据等边三角形性质求出AB=AC，根据平行线性质求出AD=AE，推出BD=BE，根据平行线性质和等腰三角形的判定求出DE=CE，即可推出答案．
点评：本题主要考查对等腰三角形的性质和判定，平行线的性质，等边三角形的性质等知识点的理解和掌握，能推出DE=CE和BD=CE是解此题的关键．