Question

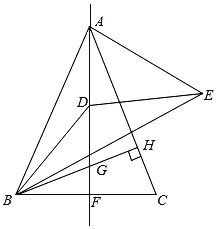
【题目】四边形ABCD是正方形，PA是过正方形顶点A的直线，作DE⊥PA于E，将射线DE绕点D逆时针旋转45°与直线PA交于点F．

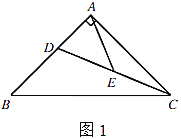
（1）如图1，当∠PAD＝45°时，点F恰好与点A重合，则的值为　 　；

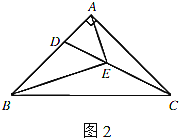
（2）如图2，若45°＜∠PAD＜90°，连接BF、BD，试求的值，并说明理由．

Answer 1

【答案】（1）；（2）＝．

【解析】

（1）由等腰直角三角形的性质可得AD＝AE，即可求解；

（2）过点B作BH⊥AP于H，由“AAS”可证△ADE≌△BAH，可得AE＝BH，由∠EFD＝45°＝∠ABD，可证点A，点F，点B，点D四点共圆，可得∠BFH＝∠ADB＝45°，即可求解．

（1）∵∠PAD＝45°，DE⊥AP，

∴∠DAE＝∠EDA，

∴AE＝DE，

∴AD＝AE，

∵四边形ABCD是正方形，

∴AD＝AB＝BF＝AE，

∴；

（2）过点B作BH⊥AP于H，

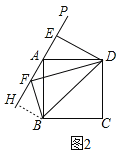
∵四边形ABCD是正方形，

∴AD＝AB，∠ABD＝45°，∠BAD＝90°，

∴∠BAH+∠DAE＝90°，

又∵∠BAH+∠ABH＝90°，

∴∠ABH＝∠DAE，

又∵AD＝AB，∠DEA＝∠AHB＝90°，

∴△ADE≌△BAH（AAS），

∴AE＝BH，

∵将射线DE绕点D逆时针旋转45°与直线PA交于点F，

∴∠EDF＝45°，

∴∠EFD＝45°＝∠ABD，

∴点A，点F，点B，点D四点共圆，

∴∠BFH＝∠ADB＝45°，

又∵BH⊥AP，

∴∠FBH＝∠BFH＝45°，

∴BH＝FH，

∴BF＝BH＝AE，

∴＝＝．