Question

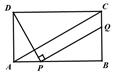
（2011湖南衡阳，26，10分）如图，在矩形ABCD中，AD=4，AB=m(m＞4)，点P是AB边上的任意一点（不与A、B重合），连结PD，过点P作PQ⊥PD，交直线BC于点Q．
(1)当m=10时，是否存在点P使得点Q与点C重合？若存在，求出此时AP的长；若不存在，说明理由；
(2)连结AC，若PQ∥AC,求线段BQ的长（用含m的代数式表示）
(3)若△PQD为等腰三角形，求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式，并写出m的取值范围．

Answer 1

【解】(1) 假设当m=10时，存在点P使得点Q与点C重合（如下图），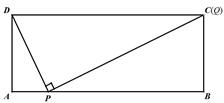

∵PQ⊥PD∴∠DPC=90°，∴∠APD＋∠BPC=90°，
又∠ADP＋∠APD=90°，∴∠BPC=∠ADP，
又∠B=∠A=90°，∴△PBC∽△DAP，∴，
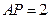∴，∴或8，∴存在点P使得点Q与点C重合，出此时AP的长2 或8．
(2)如下图，∵PQ∥AC，∴∠BPQ=∠BAC，∵∠BPQ=∠ADP，∴∠BAC=∠ADP，又∠B=∠DAP=90°，∴△ABC∽△DAP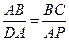，∴，即，∴．

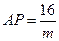∵PQ∥AC，∴∠BPQ=∠BAC，∵∠B=∠B，∴△PBQ∽△ABC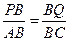，，即，∴．
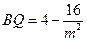(3)由已知PQ⊥PD，所以只有当DP=PQ时，△PQD为等腰三角形（如图），

∴∠BPQ=∠ADP，又∠B=∠A=90°，∴△PBQ≌△DAP，
∴PB=DA=4，AP=BQ=，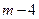
∴以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式为：S_{四边形PQCD}= S_矩形ABCD－S_△DAP－S_△QBP=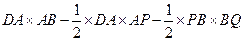
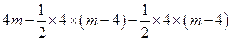==16（4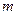＜≤8）．

解析