题目内容
如图:直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC=

52° 128°
先根据垂直的定义求出∠BOE=90°,然后求出∠BOD的度数,再根据对顶角相等求出∠AOC的度数,再根据邻补角的定义求出∠COB的度数.
解:∵OE⊥AB,
∴∠BOE=90°,
∵∠EOD=38°,
∴∠BOD=∠BOE-∠EOD=90°-38°=52°,
∴∠AOC=∠BOD=52°(对顶角相等),
解:∵OE⊥AB,
∴∠BOE=90°,
∵∠EOD=38°,
∴∠BOD=∠BOE-∠EOD=90°-38°=52°,
∴∠AOC=∠BOD=52°(对顶角相等),

练习册系列答案
相关题目


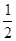 BC,
BC, 