题目内容
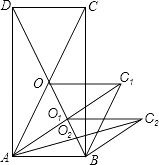
【题目】将五个边长都为2cm的正方形按如图所示摆放，点A，B，C，D分别是四个正方形的中心（对角线的交点），则图中四块阴影面积的和为（ ）
A.2cm2
B.4cm2
C.6cm2
D.8cm2
【答案】B
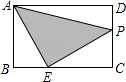
【解析】解：如图，连接AP，AN，点A是正方形的对角线的交点
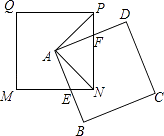
则AP=AN，∠APF=∠ANE=45°，
∵∠PAF+∠FAN=∠FAN+∠NAE=90°，
∴∠PAF=∠NAE，
∴△PAF≌△NAE，
∴四边形AENF的面积等于△NAP的面积，
而△NAP的面积是正方形的面积的 
，而正方形的面积为4，
∴四边形AENF的面积为1cm2，四块阴影面积的和为4cm2．
故答案为：B．
根据题意画出图形，连接AP，AN，点A是正方形的对角线的交点，则AP=AN，∠APF=∠ANE=45°，由∠PAF+∠FAN=∠FAN+∠NAE=90°，得到∠PAF=∠NAE，△PAF≌△NAE，得到四边形AENF的面积等于△NAP的面积，而△NAP的面积是正方形的面积的 ，而正方形的面积为4，所以四边形AENF的面积为1cm2，四块阴影面积的和为4cm2．
名校课堂系列答案【题目】某校八年级全体男同学参加了跳绳比赛，从中随机抽取某班男同学的跳绳成绩，制作了如下频数分布表：
组别 | 99.5﹣109.5 | 109.5﹣119.5 | 119.5﹣129.5 | 129.5﹣139.5 | 139.5﹣149.5 | 149.5﹣159.5 |
频数 | 2 | 4 | 8 | 7 | 3 | 1 |
根据上面统计信息，解答下列问题：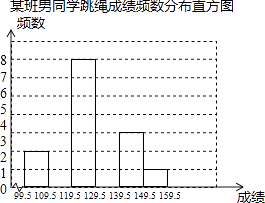
（1）补全频数分布直方图．
（2）班级准备对跳绳成绩优秀的男同学进行奖励，奖励人数占班级男同学的20%，该班张辉同学的成绩为140个，通过计算判断张辉能否获得奖励．
（3）八年级共有200名男同学，若规定男同学的跳绳成绩在120个以上（含120个）为合格，估计该校八年级男同学成绩合格的人数．
