题目内容
 如图,已知OA⊥OD,∠FOD=2∠COD,OB平分∠AOC,OE平分∠COF.
如图,已知OA⊥OD,∠FOD=2∠COD,OB平分∠AOC,OE平分∠COF.
(1)若∠COD=30°,求∠BOE的度数;
(2)若∠BOE=85°,求∠COD的度数.(提示:设∠COD=x°)
解:(1)∵∠COD=30°,OA⊥OD,∴∠AOC=60°,
∵OB平分∠AOC,∴∠BOC=30°,
∵∠FOD=2∠COD,∴∠FOD=60°,
∵OE平分∠COF,∴∠COE=45°,
∴∠BOE=30+45=75°;
(2)设∠COD=x°,由已知可得:
∠BOC= ,∠COE=
,∠COE=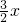 ,
,
∴ +
+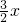 =85,解之x=40
=85,解之x=40
答:∠COD=40°.
分析:(1)根据∠COD=30°,OA⊥OD,可求出∠AOC,根据OB平分∠AOC和∠FOD=2∠COD,可求出∠FOD,再根据OE平分∠COF,求出∠COE,即可求出∠BOE;
(2)设∠COD=x°,根据已知条件可得∠BOC= ,∠COE=
,∠COE=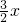 ,然后列方程,解方程即可求出答案.
,然后列方程,解方程即可求出答案.
点评:此题主要考查学生对角的计算的理解和掌握,此题涉及到方程思想,有一定拔高难度,属于中档题.
∵OB平分∠AOC,∴∠BOC=30°,
∵∠FOD=2∠COD,∴∠FOD=60°,
∵OE平分∠COF,∴∠COE=45°,
∴∠BOE=30+45=75°;
(2)设∠COD=x°,由已知可得:
∠BOC=
 ,∠COE=
,∠COE=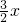 ,
,∴
 +
+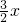 =85,解之x=40
=85,解之x=40答:∠COD=40°.
分析:(1)根据∠COD=30°,OA⊥OD,可求出∠AOC,根据OB平分∠AOC和∠FOD=2∠COD,可求出∠FOD,再根据OE平分∠COF,求出∠COE,即可求出∠BOE;
(2)设∠COD=x°,根据已知条件可得∠BOC=
 ,∠COE=
,∠COE=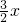 ,然后列方程,解方程即可求出答案.
,然后列方程,解方程即可求出答案.点评:此题主要考查学生对角的计算的理解和掌握,此题涉及到方程思想,有一定拔高难度,属于中档题.

练习册系列答案
相关题目
 如图,已知OA⊥OD,∠FOD=2∠COD,OB平分∠AOC,OE平分∠COF.
如图,已知OA⊥OD,∠FOD=2∠COD,OB平分∠AOC,OE平分∠COF. 如图,已知OA⊥OD,BO平分∠AOC,∠AOB:∠COD=2:5.求∠AOB的度数.
如图,已知OA⊥OD,BO平分∠AOC,∠AOB:∠COD=2:5.求∠AOB的度数.
 °)
°) 图,已知OA⊥OD,∠FOD=2∠COD,OB平分∠AOC,OE平分∠COF.
图,已知OA⊥OD,∠FOD=2∠COD,OB平分∠AOC,OE平分∠COF.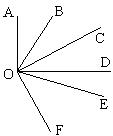
 °)
°)