题目内容
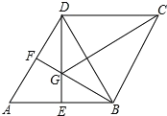
【题目】如图,在平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OA,OB,CD的中点,EG交FD于点H.则下列结论:①ED⊥CA;②EF=CG;③EH=![]() EG;④S△EFD=S△CEG成立的个数有( )
EG;④S△EFD=S△CEG成立的个数有( )

A.1个B.2个C.3个D.4个
【答案】D
【解析】
由平行四边形性质和等腰三角形“三线合一”即可得ED⊥CA,根据三角形中位线定理可得EF=![]() AB;由直角三角形斜边上中线等于斜边一半可得EG=
AB;由直角三角形斜边上中线等于斜边一半可得EG=![]() CD,即可得EF=EG;连接EG,可证四边形DEFG是平行四边形,即可得
CD,即可得EF=EG;连接EG,可证四边形DEFG是平行四边形,即可得![]() ;由三角形中位线定理可证得S△OEF=
;由三角形中位线定理可证得S△OEF=![]() S△AOB,进而可得S△EFD=S△OEF+S△ODE=
S△AOB,进而可得S△EFD=S△OEF+S△ODE=![]() SABCD+
SABCD+![]() SABCD=
SABCD=![]() SABCD,再根据E、G分别是OA、CD中点,可得S△CEG=
SABCD,再根据E、G分别是OA、CD中点,可得S△CEG=![]() S△CDE=
S△CDE=![]() SABCD,即可得S△EFD=S△CEG.
SABCD,即可得S△EFD=S△CEG.
解:如图,连接FG,
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD,AD=BC,AD∥BC,AB=CD,AB∥CD
∵BD=2AD
∴OD=AD
∵点E为OA中点
∴ED⊥CA,故①正确;
∵E,F,G分别是OA,OB,CD的中点,
∴EF∥AB,EF=![]() AB,S△OEF=
AB,S△OEF=![]() S△AOB,
S△AOB,
∵∠CED=90°,CG=DG=![]() CD
CD
∴EG=![]() CD
CD
∴EF=EG,故②正确;
∵EF∥CD,EF=DG
∴四边形DEFG是平行四边形
∴EH=HG
即![]() ,故③正确;
,故③正确;
∵S△AOB=S△AOD=![]() SABCD,S△ACD=
SABCD,S△ACD=![]() SABCD,
SABCD,
∴S△OEF=![]() SABCD,
SABCD,
∵AE=OE
∴S△ODE=![]() S△AOD=
S△AOD=![]() SABCD,
SABCD,
∴S△EFD=S△OEF+S△ODE=![]() SABCD+
SABCD+![]() SABCD=
SABCD=![]() SABCD,
SABCD,
∵![]()
∴CE=![]() AC
AC
∴S△CDE=![]() S△ACD=
S△ACD=![]() SABCD,
SABCD,
∵CG=DG
∴S△CEG=![]() S△CDE=
S△CDE=![]() SABCD,
SABCD,
∴S△EFD=S△CEG,故④正确;
故选:D.