题目内容
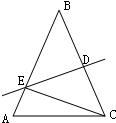
如图,在△ABC中,AB=AC=10cm,BD⊥AC于D,且BD=8cm.点M从点A出发,沿AC方向匀速运动,速度为2cm/s;同时直线PQ由点B出发沿BA方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于P,交BC于Q,连接PM,设运动时间为t(s)(0<t<5).
(1)当四边形PQCM是平行四边形时,求t的值;
(2)当t为何值时,△PQM是等腰三角形?
(3)以PM为直径作⊙E,在点P、Q整个运动过程中,是否存在这样的时刻t,使得⊙E与BC相切?若存在,请求出运动时间t的值;若不存在,请说明理由.
(1) t=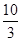 (2)t=
(2)t=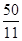 (3)存在。当t=
(3)存在。当t=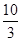 或
或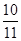 时,⊙E与BC相切
时,⊙E与BC相切
解析试题分析:(1)如图,t=10―2t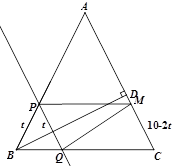
解得 t=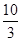
(2)①若PQ=PM,则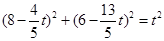
化简得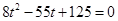 ,
,
此方程无解,舍去;
②若PQ=QM,则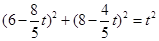 ,
,
解得t=10(舍去),t=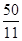
③若PM=QM,则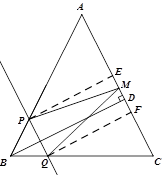
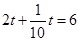 ,解得t=
,解得t=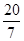
∴当t=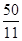 或
或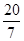 时,△PQM是等腰三角形.
时,△PQM是等腰三角形.
(3)假设存在.当⊙E与BC相切时,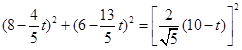
解得t=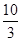 ,t=
,t=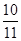 .
.
∴当t=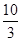 或
或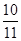 时,⊙E与BC相切.
时,⊙E与BC相切.
考点:几何图形的性质
点评:该题较为复杂,是常考题,主要考查学生对平行四边形、等腰三角形、圆与直线关系的性质以及各种数量关系的分析掌握情况。

练习册系列答案
相关题目
 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=