题目内容
 31、如图,△ACD和△ABE都是直角等腰三角形,∠DAC和∠EAB是直角,连接CE.
31、如图,△ACD和△ABE都是直角等腰三角形,∠DAC和∠EAB是直角,连接CE.(1)在图上画出△ACE以点A为旋转中心,顺时针旋转90°后得到的△AC'E'(只需作出图形;不写画法);
(2)猜想EC与C'E'的位置有什么关系,并证明你的结论.
分析:(1)根据旋转角度、旋转方向、旋转点找出各点的对应点,顺次连接即可得出;
(2)由旋转的性质可知:△AEC≌△AE′C′,故∠AEC=∠AE′C′,又∠AEC+∠CEE′+∠AE′E=90°,可得∠AE′C′+∠CEE′+∠AE′E=90°,继而可得∠EOE′=90°,从而得出EC与C'E'的位置关系.
(2)由旋转的性质可知:△AEC≌△AE′C′,故∠AEC=∠AE′C′,又∠AEC+∠CEE′+∠AE′E=90°,可得∠AE′C′+∠CEE′+∠AE′E=90°,继而可得∠EOE′=90°,从而得出EC与C'E'的位置关系.
解答:解:(1)所画图形如下所示:

(2)由旋转的性质可知:△AEC≌△AE′C′,
∴∠AEC=∠AE′C′,
又∠AEC+∠CEE′+∠AE′E=90°,
∴∠AE′C′+∠CEE′+∠AE′E=90°,
∴∠EOE′=90°,
∴EC⊥C'E'.

(2)由旋转的性质可知:△AEC≌△AE′C′,
∴∠AEC=∠AE′C′,
又∠AEC+∠CEE′+∠AE′E=90°,
∴∠AE′C′+∠CEE′+∠AE′E=90°,
∴∠EOE′=90°,
∴EC⊥C'E'.
点评:本题主要考查的是旋转变换的作图方法,在旋转作图时,一定要明确三个要素:旋转中心、旋转方向、旋转角度.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
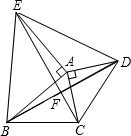 如图,△ACD和△AEB都是等腰直角三角形,∠EAB=∠CAD=90°,下列五个结论:①EC=BD;②EC⊥BD;③S四边形EBCD=
如图,△ACD和△AEB都是等腰直角三角形,∠EAB=∠CAD=90°,下列五个结论:①EC=BD;②EC⊥BD;③S四边形EBCD= 23、如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.
23、如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.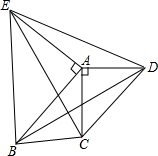 如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°.四边形ABCD是平行四边形,下列结论中错误的有( )
如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°.四边形ABCD是平行四边形,下列结论中错误的有( ) 如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,四边形ABCD是平行四边形,下列结论错误的是( )
如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,四边形ABCD是平行四边形,下列结论错误的是( )