题目内容
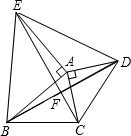 如图,△ACD和△AEB都是等腰直角三角形,∠EAB=∠CAD=90°,下列五个结论:①EC=BD;②EC⊥BD;③S四边形EBCD=
如图,△ACD和△AEB都是等腰直角三角形,∠EAB=∠CAD=90°,下列五个结论:①EC=BD;②EC⊥BD;③S四边形EBCD=| 1 | 2 |
分析:证明△ABD≌△AEC,可得到EC=BD,∠AEC=∠ABD,从而可证明EC⊥BD,从而可知道四边形EBCD的面积,根据两个角对应相等的两个三角形互为相似三角形可证明△ADE和△ABC是否相似.
解答:解:∵△ACD和△AEB都是等腰直角三角形,
∴AE=AB,AD=AC,∠EAC=∠BAD,
∴△AEC≌△ABD,
∴EC=BD,∠AEC=∠ABD,
∵∠AEB+∠ABE=90°,
∴∠FEB+∠EBF=90°,
∴EC⊥BD,
∴SEBCD=
EC•BD.
所以①②③正确.
④错误.
∵∠EBF=45°+∠ABF,∠FCD=45°+∠ACF,∠ABF≠∠ACF,
∴∠EBF≠∠FCD,
同理:∠BEF≠∠CDF.
∴△EBF和△CDF不相似.
故⑤不正确.
故答案为:①②③
∴AE=AB,AD=AC,∠EAC=∠BAD,
∴△AEC≌△ABD,
∴EC=BD,∠AEC=∠ABD,
∵∠AEB+∠ABE=90°,
∴∠FEB+∠EBF=90°,
∴EC⊥BD,
∴SEBCD=
| 1 |
| 2 |
所以①②③正确.
④错误.
∵∠EBF=45°+∠ABF,∠FCD=45°+∠ACF,∠ABF≠∠ACF,
∴∠EBF≠∠FCD,
同理:∠BEF≠∠CDF.
∴△EBF和△CDF不相似.
故⑤不正确.
故答案为:①②③
点评:本题考查了全等三角形的判定和性质,等腰直角三角形的性质,相似三角形的判定.

练习册系列答案
相关题目
 23、如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.
23、如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.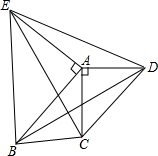 如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°.四边形ABCD是平行四边形,下列结论中错误的有( )
如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°.四边形ABCD是平行四边形,下列结论中错误的有( ) 如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,四边形ABCD是平行四边形,下列结论错误的是( )
如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,四边形ABCD是平行四边形,下列结论错误的是( ) 31、如图,△ACD和△ABE都是直角等腰三角形,∠DAC和∠EAB是直角,连接CE.
31、如图,△ACD和△ABE都是直角等腰三角形,∠DAC和∠EAB是直角,连接CE.