题目内容
【题目】在数轴上,把表示数1的点称为基准点,记作点![]() . 对于两个不同的M和N,若点M、点N到点
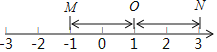
. 对于两个不同的M和N,若点M、点N到点![]() 的距离相等,则称点M与点N互为基准变换点. 例如:图中,点M表示数
的距离相等,则称点M与点N互为基准变换点. 例如:图中,点M表示数![]() ,点N表示数3,它们与基准点
,点N表示数3,它们与基准点![]() 的距离都是2个单位长度,点M与点N互为基准变换点.
的距离都是2个单位长度,点M与点N互为基准变换点.
(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
① 若a=0,则b= ;若![]() ,则b= ;
,则b= ;
② 用含a的式子表示b,则b= ;
(2)对点A进行如下操作:先把点A表示的数乘以![]() ,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是 ;
,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是 ;
(3)点P在点Q的左边,点P与点Q之间的距离为8个单位长度.对P、Q两点做如下操作:点P沿数轴向右移动k(k>0)个单位长度得到![]() ,
, ![]() 为
为![]() 的基准变换点,点
的基准变换点,点![]() 沿数轴向右移动k个单位长度得到
沿数轴向右移动k个单位长度得到![]() ,
, ![]() 为
为![]() 的基准变换点,……,依此顺序不断地重复,得到
的基准变换点,……,依此顺序不断地重复,得到![]() ,
, ![]() ,…,
,…, ![]() .
. ![]() 为Q的基准变换点,将数轴沿原点对折后
为Q的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,
, ![]() 为
为![]() 的基准变换点, 将数轴沿原点对折后
的基准变换点, 将数轴沿原点对折后![]() 的落点为
的落点为![]() ,……,依此顺序不断地重复,得到
,……,依此顺序不断地重复,得到![]() ,
, ![]() ,…,
,…, ![]() .若无论k为何值,
.若无论k为何值, ![]() 与
与![]() 两点间的距离都是4,则n= .
两点间的距离都是4,则n= .
【答案】(1)①2,-2;②![]() ;(2)
;(2)![]() ;(3)4或12.
;(3)4或12.
【解析】(1)①根据互为基准变换点的定义可得出a+b=2,代入数据即可得出结论;②根据a+b=2,变换后即可得出结论;
(2)设点A表示的数为x,根据点A的运动找出点B,结合互为基准变换点的定义即可得出关于x的一元一次方程,解之即可得出结论;
(3)根据点Pn与点Qn的变化找出变化规律“P4n=m、Q4n=m+8-4n”,再根据两点间的距离公式即可得出关于n的含绝对值符号的一元一次方程,解之即可得出结论.
解:(1)①∵点A表示数a,点B表示数b,点A与点B互为基准变换点,
∵a+b=2.
当a=0时,b=2;当a=4时,b=2.
故答案为:2;2.
②∵a+b=2,
∴b=2a.
故答案为:2a.
(2)设点A表示的数为x,
根据题意得: ![]() x3+x=2,
x3+x=2,
解得:x=![]() .
.
故答案为: ![]() .
.
(3)设点P表示的数为m,则点Q表示的数为m+8,
由题意可知:P1表示的数为m+k,P2表示的数为2(m+k),P3表示的数为2m,P4表示的数为m,P5表示的数为m+k,…,
Q1表示的数为m6,Q2表示的数为m+6,Q3表示的数为m4,Q4表示的数为m+4,Q5表示的数为m2,Q6表示的数为m+2,…,
∴P4n=m,Q4n=m+84n.
令|m(m+84n)|=4,即|84n|=4,
解得:4n=4或4n=12.
故答案为:4或12.