Question

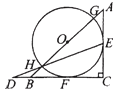
【题目】如图，在正方形ABCD内有一点P满足AP=AB，PB=PC，连接AC、PD．

求证：（1）△APB≌△DPC；（2）∠BAP=2∠PAC．

Answer 1

【答案】证明见解析.

【解析】试题分析：根据正方形的性质和等腰三角形的性质得出∠ABP=∠DCP，再利用SAS判定三角形全等即可；（2）根据已知条件和正方形的性质得到△APD为等边三角形，求得∠DAP=60，即可分别求出∠PAC、∠BAP的度数，即可得到二者关系.

试题解析：

(1)∵四边形ABCD是正方形,∴∠ABC=∠DCB=90.

∵PB=PC,∴∠PBC=∠PCB.

∴∠ABC∠PBC=∠DCB∠PCB,即∠ABP=∠DCP.

又∵AB=DC，PB=PC，

∴△APB≌△DPC.(3分)

(2)证明：∵四边形ABCD是正方形，

∴∠BAC=∠DAC=45.

∵△APB≌△DPC，∴AP=DP.

又∵AP=AB=AD，∴DP=AP=AD.

∴△APD是等边三角形。

∴∠DAP=60.

∴∠PAC=∠DAP∠DAC=15.

∴∠BAP=∠BAC∠PAC=30.

∴∠BAP=2∠PAC.