题目内容
如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s( ),则s(
),则s( )与t(s)的函数关系可用图像表示为( )
)与t(s)的函数关系可用图像表示为( )

B.
解析试题分析:根据题意BE=CF=t,CE=8-t,
∵四边形ABCD为正方形,
∴OB=OC,∠OBC=∠OCD=45°,
∵在△OBE和△OCF中 ,
,
∴△OBE≌△OCF(SAS),
∴S△OBE=S△OCF,
∴S四边形OECF=S△OBC= ×82=16,
×82=16,
∴S=S四边形OECF-S△CEF=16- (8-t)•t=
(8-t)•t= t2-4t+16=
t2-4t+16= (t-4)2+8(0≤t≤8),
(t-4)2+8(0≤t≤8),
∴s(cm2)与t(s)的函数图象为抛物线一部分,顶点为(4,8),自变量为0≤t≤8.
故选B.
考点:动点问题的函数图象.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( )
| A.y=﹣2(x+1)2+2 | B.y=﹣2(x+1)2﹣2 |
| C.y=﹣2(x﹣1)2+2 | D.y=﹣2(x﹣1)2﹣2 |
已知关于 的一元二次方程
的一元二次方程 的两个实数根分别为
的两个实数根分别为 ,
, (
( ),则二次函数
),则二次函数 中,当
中,当 时,
时, 的取值范围是( )
的取值范围是( )
A. | B.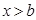 | C. | D. 或 或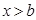 |
如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:①当x>3时,y<0;②3a+b>0;③﹣1≤a≤﹣ ;④3≤n≤4中,正确的是( )。
;④3≤n≤4中,正确的是( )。
| A.①② | B.③④ | C.①④ | D.①③ |
将二次函数 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
A. | B. |
C. | D. |
如图,正方形ABCD的边长为6cm,O是AB的中点,也是抛物线的顶点,OP⊥AB,两半圆的直径分别为OA,OB,抛物线经过C,D两点,且关于OP对称,则图中阴影部分的面积为( )(π取3.14,结果保留两位小数)
| A.7.07cm2 |
| B.3.53cm2 |
| C.14.13cm2 |
| D.10.60cm2 |


 C.2
C.2 D.2
D.2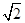 +2
+2