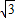Question

把一个矩形对折成两个相等的矩形后，与原来矩形相似，则原矩形长与宽之比为（　　）

• A、

  2

  +1
• B、

  2

  -1
• C、

  2

• D、

  3

Answer 1

分析：对折成两个相等的矩形，与原来矩形相似，即对应边成比例．

解答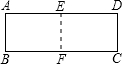：解：如图，
因为对折后的矩形与原来矩形相似，且角都为直角，所以对折后对应边成比例．
设原矩形的长为x，宽为y，折叠后的矩形的长应为y，宽变为

1

2

x，
∴有

x

y

=

y

1 2 x

，得x：y=

2

：1．
∴原矩形长与宽之比为

2

：1，
故选C．

点评：熟练掌握相似多边形的性质．