题目内容
如图,在一条公路CD的同一侧有A、B两个村庄,A、B与公路的距离AC、BD分别为500m和700m,且C、D两地相距500m,若要公路旁(在CD上)建一个车站,则A、B两村庄到车站的距离之和最短是( ).

A.1000m (B)1200m (C)1300m (D)1700m

A.1000m (B)1200m (C)1300m (D)1700m
C
本题即是要在CD上找一个点(设为点P),使AP+PB的和最小.设A′是点A关于CD的对称点,当A′、P、B三点共线时,AP+PB的和最小.
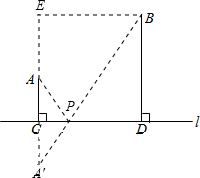
解:延长AC到A′,使A′C=AC,则A′与点A关于CD对称.
连接A′B交CD于点P,连接PA,此时AP+PB的和最小.
∵A′与点A关于CD对称,
∴PA′=PA,
∴AP+PB=A′P+PB=A′B.
过点B作AC的垂线,垂足为点E.
在直角△A′BE中,BE=CD=500m,A′E=A′C+CE=AC+BD=1200m,
由勾股定理,得A′B=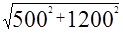 =1300m.
=1300m.
∴AP+PB=1300m.
故A、B两村庄到集贸市场的距离之和最短是1300m.
故选C.
本题主要考查轴对称--最短路线问题,作出其中一点的对称点,构造直角三角形并利用两点之间线段最短是解题的关键.

解:延长AC到A′,使A′C=AC,则A′与点A关于CD对称.
连接A′B交CD于点P,连接PA,此时AP+PB的和最小.
∵A′与点A关于CD对称,
∴PA′=PA,
∴AP+PB=A′P+PB=A′B.
过点B作AC的垂线,垂足为点E.
在直角△A′BE中,BE=CD=500m,A′E=A′C+CE=AC+BD=1200m,
由勾股定理,得A′B=
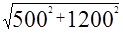 =1300m.
=1300m.∴AP+PB=1300m.
故A、B两村庄到集贸市场的距离之和最短是1300m.
故选C.
本题主要考查轴对称--最短路线问题,作出其中一点的对称点,构造直角三角形并利用两点之间线段最短是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


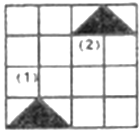


 关于直线DE对称的
关于直线DE对称的 ;
; 顺时针方向旋转90°后
顺时针方向旋转90°后 的
的 ;
;
