Question

如图，AB是半圆O的直径，过点O作弦AD的垂线交切线AC于点C，OC与半圆O交于点E，连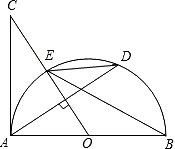接BE，DE．
（1）求证：∠BED=∠C；
（2）若OA=5，AD=8，求AC的长．

Answer 1

分析：（1）由切线的性质得∠1+∠2=90°；由同角的余角相等得到∠C=∠2．由圆周角定理知∠BED=∠2，故∠BED=∠C；
（2）连接BD．由直径直径对的圆周角是直角得∠ADB=90°，由勾股定理求得BD=

AB2-AD2

=

102-82

=6．
由△OAC∽△BDA得OA：BD=AC：DA，从而求得AC的值．

解答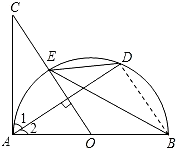：（1）证明：∵AC是⊙O的切线，AB是⊙O直径，
∴AB⊥AC．
则∠1+∠2=90°，
又∵OC⊥AD，
∴∠1+∠C=90°，
∴∠C=∠2，
而∠BED=∠2，
∴∠BED=∠C；

（2）解：连接BD，
∵AB是⊙O直径，
∴∠ADB=90°，
∴BD=

AB2-AD2

=

102-82

=6，
∴△OAC∽△BDA，
∴OA：BD=AC：DA，
即5：6=AC：8，
∴AC=

20

3

．

点评：本题利用了切线的性质，直径对的圆周角是直角，同角的余角相等，相似三角形的判定和性质求解．