题目内容
 已知一次函数y=kx+b的图象与直线
已知一次函数y=kx+b的图象与直线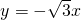 平行且经过点(2,
平行且经过点(2,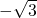 ),与x轴、y轴分别交于A、B、两点.
),与x轴、y轴分别交于A、B、两点.
(1)求此一次函数的解析式;
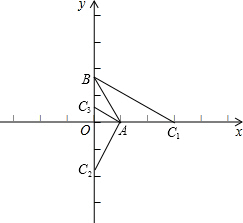
(2)点C是坐标轴上一点,若△ABC是底角为30°的等腰三角形,求点C的坐标.
 解:(1)∵一次函数y=kx+b的图象与直线
解:(1)∵一次函数y=kx+b的图象与直线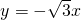 平行且经过点(2,
平行且经过点(2,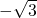 ),
),∴
 ,
,解得
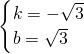 .
.∴一次函数解析式为
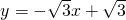 .
.(2)令y=0,则x=1;令x=0,则
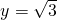 ,
,∴A(1,0),B(0,
 ).
).∵OA=1,OB=
 ,
,∴AB=2,
∴∠ABO=30°,
①若AB=AC,可求得点C的坐标为C1(3,0)或C2(0,-
 ),
),②若CB=CA,如图∠OAC3=60°-30°=30°,OC3=OA•tan30°=
 ,
,∴C3(0,
 ),
),∴C1(3,0),C2(0,-
 ),C3(0,
),C3(0, ).
).分析:(1)由于一次函数与直线
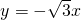 平行,则比例系数为-
平行,则比例系数为- ,设出函数解析式为y=-
,设出函数解析式为y=- x+b,将点(2,
x+b,将点(2,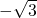 )代入解析式即可得到b的值,从而求出函数解析式;
)代入解析式即可得到b的值,从而求出函数解析式;(2)画出图形,分两种情况讨论,①AB=AC,可求得点C的坐标为C1(3,0)或C2(0,-
 ),②CB=CAC3(0,
),②CB=CAC3(0, ),找到三个不同的C点,求出不同的等腰三角形.
),找到三个不同的C点,求出不同的等腰三角形.点评:本题考查了一次函数的性质,等腰三角形的性质,关键是分类讨论思想的应用,以及三角函数的应用.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1).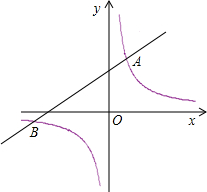 m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.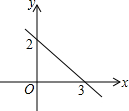 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.