题目内容
你能很快算出20052吗?为了解决这个问题,我们考察个位上的数字是5的自然数的平方,任意一个个位数为5的自然数可写成10n+5,即求(10n+5)2的值(为正整数),请分析n=1,n=2,……这些简单情况,从中探索其规律,并归纳、猜想出结论(在下面的空格内填上你探索的结果)
(1)通过计算,探索规律:
152=225 可写成100×1×(1+1)+25
252=625 可写成100×2×(2+1)+25
352=1225 可写成100×3×(3+1)+25
452=2025 可写成100×4×(4+1)+25
……
752=5625 可写成
852=7225 可写成 ;
(2)从小题(1)的结果归纳、猜想得:(10n+5)2 = ;
(3)根据上面的归纳、猜想,请计算出:20052 = .
(1)通过计算,探索规律:
152=225 可写成100×1×(1+1)+25
252=625 可写成100×2×(2+1)+25
352=1225 可写成100×3×(3+1)+25
452=2025 可写成100×4×(4+1)+25
……
752=5625 可写成
852=7225 可写成 ;
(2)从小题(1)的结果归纳、猜想得:(10n+5)2 = ;
(3)根据上面的归纳、猜想,请计算出:20052 = .
(1)100×7×(7+1)+25,100×8×(8+1)+25;
(2)100×n×(n+1)+25;
(3)100×200×(200+1)+25=4020025
(2)100×n×(n+1)+25;
(3)100×200×(200+1)+25=4020025
试题分析:(1)仔细分析所给算式的规律即可得到结果;
(2)根据(1)中的算式的规律即可得到结果;
(3)根据(2)中发现的规律即可得到结果.
(1)由题意得
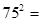 5625 可写成100×7×(7+1)+25,
5625 可写成100×7×(7+1)+25,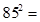 7225 可写成100×8×(8+1)+25;
7225 可写成100×8×(8+1)+25;(2)(10n+5)
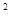 =100×n×(n+1)+25;
=100×n×(n+1)+25;(3)由题意得
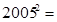 100×200×(200+1)+25=4020025.
100×200×(200+1)+25=4020025.点评:解答本题的关键是读懂所给算式的规律,再把这个规律应用于解题.

练习册系列答案
相关题目
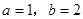
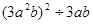 ;(2)
;(2)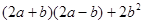
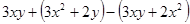 ,其中
,其中 ;
;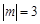 ,求
,求 的值。
的值。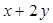 的值是-2,则代数式
的值是-2,则代数式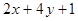 的值是( ).
的值是( ).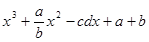 的值。
的值。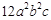 ,
,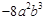 ,
,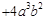 的公因式为____________
的公因式为____________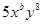 与
与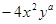 是同类项,则a+b的值是________.
是同类项,则a+b的值是________.