题目内容
【题目】如图,在△ABC中,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.
(1)求证:AE=DB;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之和等于AB的长.

【答案】(1)详见解析;(2)AE+BE=AB;BD+BE=AB;AE+AF=AB;BD+AF=AB.
【解析】
试题分析:(1)利用旋转的性质得AC=BC,∠BCA=60°,则可判断△ABC为等边三角形,过点E做EG∥AC交BC于点G,如图,则△EBG为等边三角形,所以EG=BE=BG,∠EBG=∠EGB=60°,则∠EBD=∠EGC=120°,接下来证明△BDE≌△GCE得到BD=GC,然后利用等线段代换可得到AE=DB;(2)利用BD=AE,BE=BC=CE=EF等线段代换易得四对线段,使每对线段长度之和等于AB的长.
试题解析: (1)∵△BCE绕点C顺时针旋转60°至△ACF,
∴AC=BC,∠BCA=60°,
∴△ABC为等边三角形,
过点E做EG∥AC交BC于点G,如图,
∴△EBG为等边三角形,
∴EG=BE=BG,∠EBG=∠EGB=60°,
∴∠EBD=∠EGC=120°,
∵ED=EC
∴∠D=∠ECD,
在△BDE和△GCE中
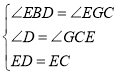 ,
,
∴△BDE≌△GCE,
∴BD=GC,
∵△ABC为等边三角形,
∴AB=BC,
∴AB﹣BE=BC﹣BG,
∴AE=CG,
∴AE=DB;
(2)AE+BE=AB;BD+BE=AB;AE+AF=AB;BD+AF=AB.


练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
