Question

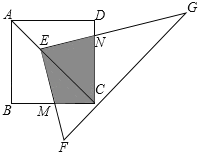
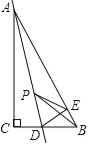
【题目】如图，在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=1，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是 ．

Answer 1

【答案】1+.

【解析】

试题解析：连接CE，交AD于M，

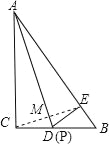
∵沿AD折叠C和E重合，

∴∠ACD=∠AED=90°，AC=AE，∠CAD=∠EAD，

∴AD垂直平分CE，即C和E关于AD对称，CD=DE=1，

∴当P和D重合时，PE+BP的值最小，即此时△BPE的周长最小，最小值是BE+PE+PB=BE+CD+DB=BC+BE，

∵∠DEA=90°，

∴∠DEB=90°，

∵∠B=60°，DE=1，

∴BE=，BD=，

即BC=1+，

∴△PEB的周长的最小值是BC+BE=1++=1+.