题目内容
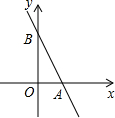 一次函数y=-2x+4的图象如图,图象与x轴交于点A,与y轴交于点B.
一次函数y=-2x+4的图象如图,图象与x轴交于点A,与y轴交于点B.
(1)求A、B两点坐标.
(2)求图象与坐标轴所围成的三角形的面积是多少.
解:(1)对于y=-2x+4,
令y=0,得
-2x+4,
∴x=2;
∴一次函数y=-2x+4的图象与x轴的交点A的坐标为(2,0);
令x=0,得
y=4.
∴一次函数y=-2x+4的图象与y轴的交点B的坐标为(0,4);
(2)S△AOB= •OA•OB=
•OA•OB= ×2×4=4.
×2×4=4.
∴图象与坐标轴所围成的三角形的面积是4.
分析:(1)x轴上所有的点的坐标的纵坐标均为0;y轴上所有的点的坐标的横坐标均为0;
(2)利用(1)中所求的点A、B的坐标可以求得OA、OB的长度;然后根据三角形的面积公式可以求得△OAB的面积.
点评:本题考查了三角形的面积、一次函数图象上点的坐标特征.一次函数y=ax+b(a≠0)图象上所有点的坐标均满足该解析式.
令y=0,得
-2x+4,
∴x=2;
∴一次函数y=-2x+4的图象与x轴的交点A的坐标为(2,0);
令x=0,得
y=4.
∴一次函数y=-2x+4的图象与y轴的交点B的坐标为(0,4);
(2)S△AOB=
 •OA•OB=
•OA•OB= ×2×4=4.
×2×4=4.∴图象与坐标轴所围成的三角形的面积是4.
分析:(1)x轴上所有的点的坐标的纵坐标均为0;y轴上所有的点的坐标的横坐标均为0;
(2)利用(1)中所求的点A、B的坐标可以求得OA、OB的长度;然后根据三角形的面积公式可以求得△OAB的面积.
点评:本题考查了三角形的面积、一次函数图象上点的坐标特征.一次函数y=ax+b(a≠0)图象上所有点的坐标均满足该解析式.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
一次函数y=2x-3与x轴的交点( )
A、(
| ||
B、(-
| ||
| C、(3,0) | ||
| D、(-3,0) |
下列命题中,假命题的是( )
| A、在S=πR2中,S和R2成正比例 | ||
| B、函数y=x2+2x-1的图象与x轴只有一个交点 | ||
| C、一次函数y=-2x-1的图象经过第二、三、四象限 | ||
D、在函数y=-
|