题目内容
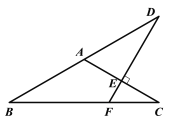
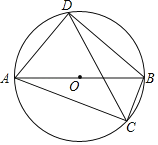
【题目】如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F.
(1)求证:DF是⊙O的切线;
(2)过点F作FG⊥AB,垂足为G,若AB=12.
①求FG的长;
②求点D到FG的距离.

【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接OD,证∠ODF=90°即可.
(2)利用△CDF是30°的直角三角形可求得CF长,同理可利用△FGA中的60°的三角函数值可求得FG长.
(3)过D作DH⊥AB于H.利用△BDH是30°的直角三角形可求得BH长,同理可求得AG,然后根据GH=AB-AG-BH求得即可
解:(1)连接OD,∵OB=OD,∠OBD=60°,

∴△OBD为等边三角形,
∴∠ODB=∠C=60°,
∴OD∥AC,
又∵DF⊥AC,∴DF⊥OD,
∴DF是⊙O的切线;
(2)由(1)得:OD∥AC,∵O为AB的中点,
∴OD是△ABC的中位线,
∴CD=BD=![]() AB=6,
AB=6,
∴DF=CD·sin60°=![]() ,
,
CF=CD·cos60°=3,
∴AF=AC-CF=9,
∴FG=AF·sin60°=![]() ;
;
(3)如图2,过D作DH⊥AB于H.
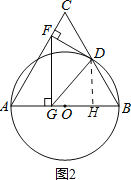
∵FG⊥AB,DH⊥AB,
∴FG∥DH,
在Rt△BDH中,∠B=60°,
∴∠BDH=30°,
∴BH=![]() BD=3,DH=
BD=3,DH=![]() BH=3
BH=3![]() .
.
在Rt△AFG中,∵∠AFG=30°,
∴AG=![]() AF=
AF=![]() ,
,
∵GH=AB-AG-BH=12-![]() -3=
-3=![]() ,
,
FG⊥AB,∴点D到FG的距离是![]() .
.

 名校课堂系列答案
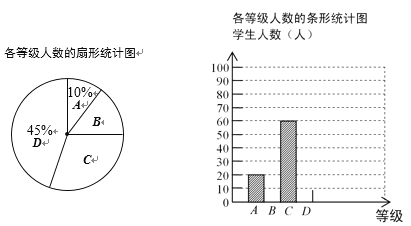
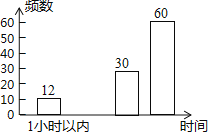
名校课堂系列答案【题目】某市教育主管部门为了解学生的作业量情况,随机抽取了几所中学八年级的部分学生进行了一次调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图、表中所提供的信息解答下列问题:
(1)本次共抽取了 名学生进行调查;
(2)x= ,y= ,补全条形统计图;
(3)若这几所中学八年级的学生共有3200人,请估计做作业时间在2小时以上的学生人数是多少?
(4)由图表可知,这次被调查的八年级学生的作业时间的中位数一定落在1.5小时﹣2小时这一时段内,你认为这种判断正确吗?(不需要说明理由)
写作业时间 | 频数 | 频率 |
1小时以内 | 12 | 0.1 |
1﹣1.5 | x | 0.15 |
1.5﹣2 | 30 | 0.25 |
2小时以上 | 60 | y |
【题目】某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?