题目内容
【题目】如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
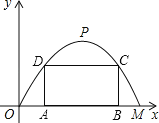
(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形“支撑架”AD﹣DC﹣CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
【答案】(1)M(12,0),P(6,6).(2)y=﹣![]() x2+2x.(3)当m=3米时,AD+DC+CB有最大值为15米.
x2+2x.(3)当m=3米时,AD+DC+CB有最大值为15米.
【解析】
试题分析:(1)根据所建坐标系易求M、P的坐标;
(2)可设解析式为顶点式,把O点(或M点)坐标代入求待定系数求出解析式;
(3)总长由三部分组成,根据它们之间的关系可设A点坐标为(m,0),用含m的式子表示三段的长,再求其和的表达式,运用函数性质求解.
解:(1)M(12,0),P(6,6).(2分)
(2)设抛物线解析式为:
y=a(x﹣6)2+6 (3分)
∵抛物线y=a(x﹣6)2+6经过点(0,0)
∴0=a(0﹣6)2+6,即a=﹣![]() (4分)
(4分)
∴抛物线解析式为:y=﹣![]() (x﹣6)2+6,即y=﹣
(x﹣6)2+6,即y=﹣![]() x2+2x.(5分)
x2+2x.(5分)
(3)设A(m,0),则B(12﹣m,0),C(12﹣m,﹣![]() m2+2m)
m2+2m)
D(m,﹣![]() m2+2m).(6分)
m2+2m).(6分)
∴“支撑架”总长AD+DC+CB=(﹣![]() m2+2m)+(12﹣2m)+(﹣
m2+2m)+(12﹣2m)+(﹣![]() m2+2m)
m2+2m)
=﹣![]() m2+2m+12
m2+2m+12
=﹣![]() (m﹣3)2+15.(8分)
(m﹣3)2+15.(8分)
∵此二次函数的图象开口向下.
∴当m=3米时,AD+DC+CB有最大值为15米.(9分)

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目