��Ŀ����
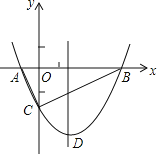
����Ŀ����֪��ͼ����COD=90����ֱ��AB��OC���ڵ�B����OD���ڵ�A������OE������AF���ڵ�G��
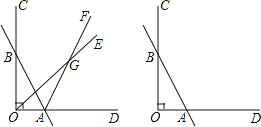
��1����OEƽ����BOA��AFƽ����BAD����OBA=30��������OGA= .
��2������GOA=![]() ��BOA����GAD=
��BOA����GAD=![]() ��BAD����OBA=30��������OGA= .
��BAD����OBA=30��������OGA= .
��3������2��������OBA=30�㡱��Ϊ����OBA=�����������������䣬����OGA= ���ú����Ĵ���ʽ��ʾ��
��4����OE����BOA�ֳ�1��2�����֣�AFƽ����BAD����ABO=����30��������90����������OGA�Ķ������ú����Ĵ���ʽ��ʾ��
���𰸡���1��15������2��10������3��![]() ������4��
������4��![]() ��+15����
��+15����![]() ��-15����
��-15����
��������
�����������1��������BAD=��ABO+��BOA=��+90������AFƽ����BAD�õ���FAD=![]() ��BAD������FAD=��EOD+��OGA��2��45��+2��OGA=��+90��������OGA=
��BAD������FAD=��EOD+��OGA��2��45��+2��OGA=��+90��������OGA=![]() ����Ȼ�����=30��������㼴�ɣ�
����Ȼ�����=30��������㼴�ɣ�
��2��������GOA=![]() ��BOA=30������GAD=
��BOA=30������GAD=![]() ��BAD����OBA=����������FAD=��EOD+��OGA�õ�3��30��+3��OGA=��+90��������OGA=
��BAD����OBA=����������FAD=��EOD+��OGA�õ�3��30��+3��OGA=��+90��������OGA=![]() ����Ȼ�����=30��������㣻
����Ȼ�����=30��������㣻
��3���ɣ�2���õ���OGA=![]() ����
����
��4�����ۣ�����EOD����COE=1��2ʱ��������BAD=��ABO+��BOA=��+90������FAD=��EOD+��OGA�õ�2��30��+2��OGA=��+90��������OGA=![]() ��+15����
��+15����
����EOD����COE=2��1ʱ������EOD=60����ͬ������OGA=![]() ��-15����
��-15����
�����������1��15����

��2��10����
��3��![]() ����
����
��4������EOD����COE=1��2ʱ��
����EOD=30����
�ߡ�BAD=��ABO+��BOA=��+90����
��AFƽ����BAD��
���FAD=![]() ��BAD��
��BAD��
�ߡ�FAD=��EOD+��OGA��
��2��30��+2��OGA=��+90����
���OGA=![]() ��+15����
��+15����
����EOD����COE=2��1ʱ������EOD=60����
ͬ���õ���OGA=![]() ��-15����
��-15����
����OGA�Ķ���Ϊ![]() ��+15����
��+15����![]() ��-15����
��-15����

 ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д�����Ŀ������ij��ѧ�ߡ����꼶��ѡ��10��ѡ�ֲμ�ѧУ�ٰ�������Ҿ�����֪ʶ�������Ʒֲ���10���ƣ�ѡ�ֵ÷־�Ϊ�������ɼ��ﵽ6�ֻ�6������Ϊ�ϸﵽ9�ֻ�10��Ϊ���㣮��ξ������ߡ����꼶��֧������ѡ�ֳɼ��ֲ�������ͳ��ͼ�ͳɼ�ͳ�Ʒ��������£��������꼶�����ӵ�6�֡�10�ֵ�ѡ�������ֱ�Ϊa��b��
�ӱ� | ƽ���� | ��λ�� | ���� | �ϸ��� | ������ |
���꼶 | 6.7 | m | 3.41 | 90% | n |
���꼶 | 7.1 | 7.5 | 1.69 | 80% | 10% |
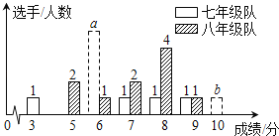
��1��������ͼ���е����ݣ���a��b��ֵ��
��2��ֱ��д�����е�m��n��ֵ��
��3������˵���꼶�ĺϸ��ʡ������ʾ����ڰ��꼶���������꼶�ӳɼ��Ȱ��꼶�Ӻã���Ҳ����˵���꼶�ӳɼ������꼶�Ӻã������������֧�ְ��꼶�ӳɼ��õ����ɣ�