题目内容
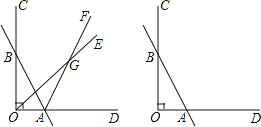
【题目】如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( )

A.2![]() B.4
B.4![]() C.4 D.8
C.4 D.8
【答案】B
【解析】
试题分析:由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形ADF与三角形ECF全等,得出AF=EF,即可求出AE的长.
解:∵AE为∠DAB的平分线,
∴∠DAE=∠BAE,
∵DC∥AB,
∴∠BAE=∠DFA,
∴∠DAE=∠DFA,
∴AD=FD,
又F为DC的中点,
∴DF=CF,
∴AD=DF=![]() DC=
DC=![]() AB=2,
AB=2,
在Rt△ADG中,根据勾股定理得:AG=![]() ,
,
则AF=2AG=2![]() ,
,
∵平行四边形ABCD,
∴AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
在△ADF和△ECF中,
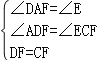 ,
,
∴△ADF≌△ECF(AAS),
∴AF=EF,
则AE=2AF=4![]() .
.
故选:B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目