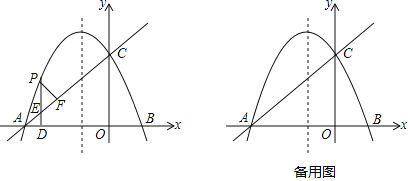题目内容
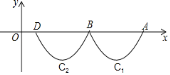
【题目】如图，抛物线
与x轴交于点A、B，把抛物线在x轴及其下方的部分记作C1，将C1向左平移得到C2，C2与x轴交于点B、D，若直线y＝
x+m与C1、C2共有3个不同的交点，则m的取值范围是（ ）
A.
B.
C.
D.
【答案】C
【解析】
首先求出点A和点B的坐标，然后求出C2解析式，分别求出直线
与抛物线C2相切时m的值以及直线过点B时m的值，结合图形即可得到答案.
解：∵抛物线
与x轴交于点A、B，
∴B（5，0），A（9，0）
∴抛物线向左平移4个单位长度
∴平移后解析式
，
当直线过B点，有2个交点，
∴
，
∴
；
当直线与抛物线C2相切时，有2个交点，
∴
，
∴x2-7x+5-2m=0，
∵直线与抛物线相切，
∴△=49-20+8m=0，
∴
；
如图，
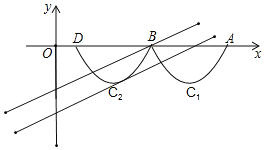
∵若直线与C1、C2共有3个不同的交点，
∴
；
故选：C．
快乐小博士巩固与提高系列答案【题目】超市有
，
两种型号的瓶子，其容量和价格如表，小张买瓶子用来分装15升油（瓶子都装满，且无剩油）；当日促销活动：购买型瓶3个或以上，一次性返还现金5元，设购买型瓶
（个），所需总费用为
（元），则下列说法不一定成立的是（ ）
型号 | A | B |
单个盒子容量（升） | 2 | 3 |
单价（元） | 5 | 6 |
A.购买型瓶的个数是
为正整数时的值B.购买型瓶最多为6个
C.与之间的函数关系式为
D.小张买瓶子的最少费用是28元
【题目】某社区组织了以“奔向幸福，‘毽’步如飞”为主题的踢毽子比赛活动，初赛结束后有甲、乙两个代表队进入决赛，已知每队有5名队员，按团体总数排列名次，在规定时间内每人踢100个以上(含100)为优秀．下表是两队各队员的比赛成绩．
1 号 | 2 号 | 3 号 | 4 号 | 5 号 | 总数 | |
甲队 | 103 | 102 | 98 | 100 | 97 | 500 |
乙队 | 97 | 99 | 100 | 96 | 108 | 500 |
经统计发现两队5名队员踢毽子的总个数相等，按照比赛规则，两队获得并列第一．学习统计知识后，我们可以通过考查数据中的其它信息作为参考，进行综合评定：
（1）甲、乙两队的优秀率分别为 ；
（2）甲队比赛数据的中位数为 个；乙队比赛数据的中位数为 个；
（3）分别计算甲、乙两队比赛数据的方差；
（4）根据以上信息，你认为综合评定哪一个队的成绩好？简述理由．
