题目内容
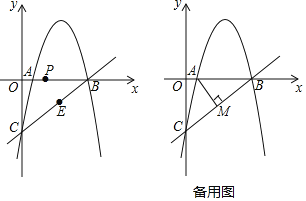
【题目】如图1,AB是O的直径,点C在O上,且点C为弧BE的中点,连接AE并延长交BC延长线于点D.

(1)判断△ABD的形状,并说明理由;
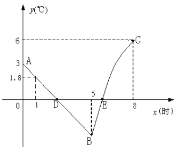
(2)过点C作CM⊥AD,垂足为点F,如图2.求证:CF是O的切线;
(3)若O的半径为3,DF=1,求sinB的值。
【答案】(1)见解析
(2)见解析
(3)![]()
【解析】
(1)如图1,连接AC,由AB是 O的直径,得到AC⊥BD,根据BC的弧=CE的弧,得到∠BAC=∠DAC,求得AB=AD;
(2)如图2,连接AC,OC,证明过半径的外端点垂直于这条半径的直线是圆的切线;
(3)由相似三角形求得BC,根据勾股定理得到AC,求得∠B的正弦.
(1)如图1,连接AC,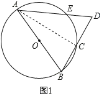
∵AB是O的直径,
∴∠ACB=90
∴AC⊥BD,
∵BC的弧=CE的弧
∴∠BAC=∠DAC,
∴AB=AD,
∴△ABD是等腰三角形;
(2)如图2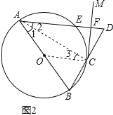 连接AC,OC,
连接AC,OC,
∵OA=OC,
∴∠1=∠3,
∵∠2=∠1,
∴∠2=∠3,
∵CF⊥AD,
∴∠AFC=90,
∴∠2+∠ACF=90
∴∠3+∠ACF=90
∴AC⊥CF,
∴CF是O的切线;
(3)∵∠ACB=∠CFD=90,
∠B=∠D,
∴△ABC∽△CDF,
∴![]() ,
,
∴![]()
∴BC=CD=![]() ,
,
∴AC=![]() ,
,
∴sinB=![]()

【题目】某品牌笔记本电脑的售价是5000元/台。最近,该商家对此型号笔记本电脑举行促销活动,有两种优惠方案。方案一:每台按售价的九折销售;方案二:若购买不超过5台,每台按售价销售;若超过5台,超过的部分每台按售价的八折销售。
设公司一次性购买此型号笔记本电脑![]() 台。
台。
Ⅰ.根据题意,填写下表:
购买台数 | 3 | 10 | 20 | … |
方案一的总费用(元) | 13500 | 45000 | 90000 | … |
方案二的总费用(元) | 15000 | … |
Ⅱ.设选择方案一的费用为![]() 元,选择方案二的费用为
元,选择方案二的费用为![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
Ⅲ.当![]() 时,该公司采用哪种方案购买更合算?并说明理由。
时,该公司采用哪种方案购买更合算?并说明理由。