题目内容
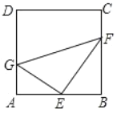
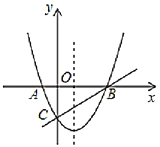
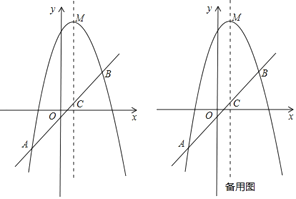
【题目】二次函数![]() 的图象交x轴于A(-1, 0),B(4, 0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC.设运动的时间为t秒.
的图象交x轴于A(-1, 0),B(4, 0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC.设运动的时间为t秒.
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接BD,当![]() 时,求△DNB的面积;
时,求△DNB的面积;
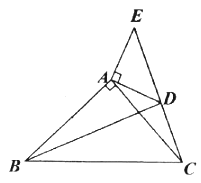
(3)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,直接写出此时点D的坐标.

【答案】(1)![]() ;(2)2;(3)(1,0)或(3,0) D(1,3)或(3,2)
;(2)2;(3)(1,0)或(3,0) D(1,3)或(3,2)
【解析】
(1)将A、B的坐标代入解答即可.
(2)先求出BC的解析式![]() ,再将x=2代入
,再将x=2代入![]() 和
和![]() ,得出D、N的坐标即可求出DN的值,再根据三角形的面积公式计算出答案即可.
,得出D、N的坐标即可求出DN的值,再根据三角形的面积公式计算出答案即可.
(3)由BM的值得出M的坐标![]() ,设P(2t-1,m),由勾股定理可得
,设P(2t-1,m),由勾股定理可得![]() ,根据题意PB=PC,所以
,根据题意PB=PC,所以![]() ,得出P的坐标为
,得出P的坐标为![]() ,PC⊥PB故
,PC⊥PB故![]() ,解得t=1或t=2,即得出答案.
,解得t=1或t=2,即得出答案.
(1)将A(-1, 0),B(4, 0)代入![]() 中,得:
中,得:
![]()
解得: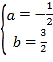
故二次函数的表达式为:![]()
(2)![]()
![]() AM=3
AM=3
又![]()
![]()
设BC的表达式为![]()
将点C(0,2),B(4,0)代入得:
![]()
解得: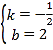
故直线BC的解析式为:![]()
将x=2代入![]() 和
和![]() ,
,
得D(2,3),N(2,1)
![]()
![]()
![]()
(3)![]()
![]()
设P(2t-1,m)
![]()
![]() ,且PB=PC
,且PB=PC
![]()
![]()
![]()
![]() PC⊥PB
PC⊥PB
![]()
![]() t=1或t=2
t=1或t=2
![]() 或者
或者![]()
![]() D(1,3)或者D(3,2)
D(1,3)或者D(3,2)

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
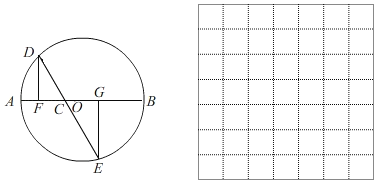
小学课时特训系列答案【题目】如图,AB是⊙O的直径,AB=4cm,C为AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=60°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=xcm,DE=ycm(当x的值为0或3时,y的值为2),探究函数y随自变量x的变化而变化的规律.
(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.40 | 0.55 | 1.00 | 1.80 | 2.29 | 2.61 | 3 |
y/cm | 2 | 3.68 | 3.84 | 3.65 | 3.13 | 2.70 | 2 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:点F与点O重合时,DE长度约为 cm(结果保留一位小数).
【题目】小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数 | 购买数量(件 | 购买总费用(元 | |
A | B | ||
第一次 | 2 | 1 | 55 |
第二次 | 1 | 3 | 65 |
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.