题目内容
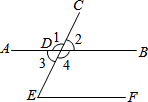
如图，直线AB与CE交于D，且∠1+∠E=180°．求证：AB∥EF．（可用多种方法）分析：方法一：由对顶角相等，结合已知条件可以判定同旁内角∠4+∠E=180°，所以易证得结论；
方法二：由邻补角的定义、结合已知条件可以判定同位角∠2=∠E，所以易证得结论；
方法三：由邻补角的定义、结合已知条件可以判定内错角角∠3=∠E，所以易证得结论．
方法二：由邻补角的定义、结合已知条件可以判定同位角∠2=∠E，所以易证得结论；
方法三：由邻补角的定义、结合已知条件可以判定内错角角∠3=∠E，所以易证得结论．
解答：证明：方法一：∵∠1+∠E=180°，∠1=∠4，
∴∠4+∠E=180°，
∴AB∥EF；
方法二：∵∠1+∠E=180°，∠1+∠2=180°
∴∠2=∠E，
∴AB∥EF；
方法三：∵∠1+∠E=180°，∠1+∠3=180°，
∴∠3=∠E，
∴AB∥EF．
∴∠4+∠E=180°，
∴AB∥EF；
方法二：∵∠1+∠E=180°，∠1+∠2=180°
∴∠2=∠E，
∴AB∥EF；
方法三：∵∠1+∠E=180°，∠1+∠3=180°，
∴∠3=∠E，
∴AB∥EF．
点评：本题考查了平行线的判定．解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
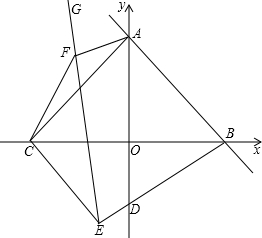
如图，直线AB、CD被直线CE所截．
