题目内容
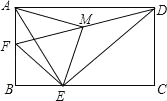
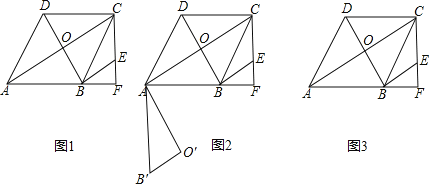
【题目】如图1,在菱形ABCD中,∠DAB=60°,AB=8![]() ,对角线交于点O,CF垂直AB交AB的延长线于点F,过点B作BE∥AC交FC于EF.
,对角线交于点O,CF垂直AB交AB的延长线于点F,过点B作BE∥AC交FC于EF.
(1)求BE的长:
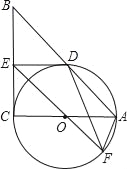
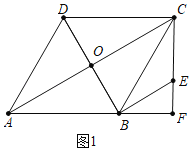
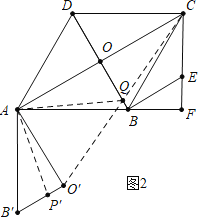
(2)如图2,在OB上有一动点P,将△AOB绕A点顺时针旋转90°至△AOB',P点的对应点为P′,现有一动点Q从P点出发,沿着适当路径先运动到O′点,再沿O′A运动至A点,再从A点沿适当的路径运动至P′点.求Q点的最短运动路径的长;
(3)若△ABO以每秒2![]() 个单位长度的速度沿射线AB向右平移,得到三角形△A1B1O1,当A1与点F重合时停止移动,设运动时间为t,在这个过程中,点O1关于直线BC的对称点为O″,当O″,F,C三点构成的三角形为等腰三角形时,直接写出t的值.
个单位长度的速度沿射线AB向右平移,得到三角形△A1B1O1,当A1与点F重合时停止移动,设运动时间为t,在这个过程中,点O1关于直线BC的对称点为O″,当O″,F,C三点构成的三角形为等腰三角形时,直接写出t的值.
【答案】(1)8;(2)12![]() 12;(3)t=2或2
12;(3)t=2或2![]() 或6s
或6s
【解析】
(1)根据菱形的性质和已知边、已知角,可证得△BCF、△BEF均是一角为30°的直角三角形,继而可求BE的长;
(2)根据菱形的性质,连接CO′交BD于Q,连接AQ,可得Q点的最短路径=QO′+O′A +AP′=CQ+QO′+AO=CO′+AO′,再根据勾股定理即可求解;
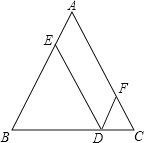
(3)①当点B1与F重合时,如图3所示,点O1在BC的中点,△O″FC为等腰三角形,可得t![]() 2s;②如图4所示,当FC=FO″时,△O″FC为等腰三角形,易证四边形HO1B1F是平行四边形,t
2s;②如图4所示,当FC=FO″时,△O″FC为等腰三角形,易证四边形HO1B1F是平行四边形,t![]() 2
2![]() s;③如图5所示,当点A1与F重合时, CF=CO″,△O″FC为等腰三角形,t=6s.
s;③如图5所示,当点A1与F重合时, CF=CO″,△O″FC为等腰三角形,t=6s.
解:(1)如图1中,
∵四边形ABCD是菱形,∠DAB=60°,
∴AB=BC=8![]() ,∠BAC=∠BCA=30°,
,∠BAC=∠BCA=30°,
∵BC∥AD,BE∥AC,
∴∠CBF=∠DAB=60°,∠BCA=∠CBE=30°,
∵CF⊥BF,
∴∠F=90°,
∴∠BCE=∠EBC=30°,
∴BE=EC,
在Rt△BCF中,BF![]() BC=4
BC=4![]() ,
,
在Rt△BEF中,cos30°![]() ,
,
∴BE=![]() =8.
=8.
(2)如图2中,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,
∴A、C关于BD对称,
连接CO′交BD于Q,连接AQ,此时Q点的运动路径最短,
最短路径=QO′+O′A+AP′=CQ+QO′+AO=CO′+AO′![]() 12=12
12=12![]() 12.
12.
(3)①如图3中,当点B1与F重合时,点O1在BC的中点,易知AA1![]() AB=4
AB=4![]() ,
,
∴t![]() 2s.
2s.

②如图4中,当FC=FO″时,设FO″交BC于H,易证四边形HO1B1F是平行四边形,
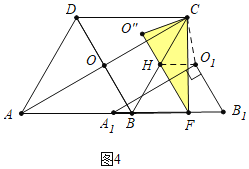
FH![]() BC=4
BC=4![]() ,HO″=HO1=B1F=12﹣4
,HO″=HO1=B1F=12﹣4![]() ,
,
∴AA1=12,t![]() 2
2![]() s.
s.
③如图5,当点A1与F重合时,CF=CO″,此时AA1=12![]() ,t=6s.
,t=6s.
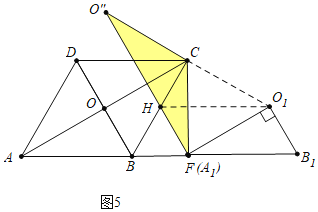
综上所述,当t=2或2![]() 或6s时,△CFO″是等腰三角形.
或6s时,△CFO″是等腰三角形.

【题目】一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
A | B | C | D | E | 平均分 | 方差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| 2 |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
|
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差.
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?