题目内容
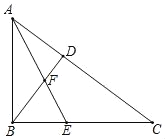
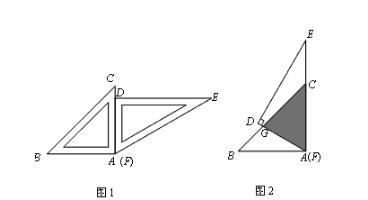
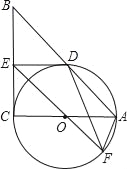
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)若⊙O的半径为3,ED=4,EO的延长线交⊙O于F,连DF、AF,求△ADF的面积.
【答案】(1)见解析;(2)△ADF的面积是![]() .
.
【解析】试题分析:(1)连接OD,CD,求出∠BDC=90°,根据OE∥AB和OA=OC求出BE=CE,推出DE=CE,根据SSS证△ECO≌△EDO,推出∠EDO=∠ACB=90°即可;
(2)过O作OM⊥AB于M,过F作FN⊥AB于N,求出OM=FN,求出BC、AC、AB的值,根据sin∠BAC=![]() ,求出OM,根据cos∠BAC=
,求出OM,根据cos∠BAC=![]() ,求出AM,根据垂径定理求出AD,代入三角形的面积公式求出即可.
,求出AM,根据垂径定理求出AD,代入三角形的面积公式求出即可.
试题解析:
(1)证明:连接OD,CD,

∵AC是⊙O的直径,
∴∠CDA=90°=∠BDC,
∵OE∥AB,CO=AO,
∴BE=CE,
∴DE=CE,
∵在△ECO和△EDO中
 ,
,
∴△ECO≌△EDO,
∴∠EDO=∠ACB=90°,
即OD⊥DE,OD过圆心O,
∴ED为⊙O的切线.
(2)过O作OM⊥AB于M,过F作FN⊥AB于N,

则OM∥FN,∠OMN=90°,
∵OE∥AB,
∴四边形OMFN是矩形,
∴FN=OM,
∵DE=4,OC=3,由勾股定理得:OE=5,
∴AC=2OC=6,
∵OE∥AB,
∴△OEC∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴AB=10,
在Rt△BCA中,由勾股定理得:BC=![]() =8,
=8,
sin∠BAC=![]() ,
,
即![]() ,
,
OM=![]() =FN,
=FN,
∵cos∠BAC=![]() ,
,
∴AM=![]()
由垂径定理得:AD=2AM=![]() ,
,
即△ADF的面积是![]() AD×FN=
AD×FN=![]() ×
×![]() ×
×![]() =
=![]() .
.
答:△ADF的面积是![]() .
.

【题目】(本小题满分10分)
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成![]() 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究![]() 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当![]() 时,
时,![]()
用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当![]() 时,
时,![]()
用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
综上所述,可得表①
| 3 | 4 | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二:
用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用![]() 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设![]() 分别等于
分别等于![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)