题目内容
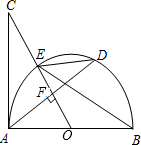
 如图,AB是半圆O的直径,C、D、E三点在半圆上,H、K是直径AB上的点,若∠AHC=∠DHB,∠DKA=∠EKB,已知弧AC为30°,弧BE为70°,则∠HDK=
如图,AB是半圆O的直径,C、D、E三点在半圆上,H、K是直径AB上的点,若∠AHC=∠DHB,∠DKA=∠EKB,已知弧AC为30°,弧BE为70°,则∠HDK=
- A.30°
- B.40°
- C.70°
- D.80°
B
分析:如果将半圆O补全,得圆O.过点D作DF⊥AB于P,交⊙O于F,连接HF、FK.首先由垂径定理,可得DP=FP,则AB是DF的垂直平分线,由线段的垂直平分线的性质得出HD=HF,KD=KF,再由等腰三角形的性质可得∠HDF=∠HFD,∠KDF=∠KFD.然后根据平角的定义证明C、H、F三点共线,E、K、F三点共线.从而∠HDK=∠CFE,最后由圆周角定理求出∠HDK的度数.
解答: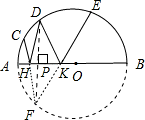 解:将半圆O补全,得圆O.过点D作DF⊥AB于P,交⊙O于F,连接HF、FK.
解:将半圆O补全,得圆O.过点D作DF⊥AB于P,交⊙O于F,连接HF、FK.
∵DF⊥AB于P,AB是圆O的直径,
∴DP=FP,
∴AB是DF的垂直平分线,
∴HD=HF,KD=KF,
∴∠HDF=∠HFD,∠KDF=∠KFD.
∵HD=HF,DP=FP,
∴∠FHB=∠DHB,
∵∠AHC=∠DHB,
∴∠FHB=∠AHC,
∴∠AHC+∠AHF=∠FHB+∠AHF=180°,
∴C、H、F三点共线.
同理,E、K、F三点共线.
∴∠HDK=∠HDF+∠KDF=∠HFD+∠KFD=∠CFE,
又∵弧AC为30°,弧BE为70°,
∴弧CE为180°-30°-70°=80°,
∴∠CFE= ×80°=40°,
×80°=40°,
∴∠HDK=40°.
故选B.
点评:本题主要考查了垂径定理,线段垂直平分线、等腰三角形的性质,圆周角定理及三点共线的证明方法.综合性强,有一定难度.
分析:如果将半圆O补全,得圆O.过点D作DF⊥AB于P,交⊙O于F,连接HF、FK.首先由垂径定理,可得DP=FP,则AB是DF的垂直平分线,由线段的垂直平分线的性质得出HD=HF,KD=KF,再由等腰三角形的性质可得∠HDF=∠HFD,∠KDF=∠KFD.然后根据平角的定义证明C、H、F三点共线,E、K、F三点共线.从而∠HDK=∠CFE,最后由圆周角定理求出∠HDK的度数.
解答:
 解:将半圆O补全,得圆O.过点D作DF⊥AB于P,交⊙O于F,连接HF、FK.
解:将半圆O补全,得圆O.过点D作DF⊥AB于P,交⊙O于F,连接HF、FK.∵DF⊥AB于P,AB是圆O的直径,
∴DP=FP,
∴AB是DF的垂直平分线,
∴HD=HF,KD=KF,
∴∠HDF=∠HFD,∠KDF=∠KFD.
∵HD=HF,DP=FP,
∴∠FHB=∠DHB,
∵∠AHC=∠DHB,
∴∠FHB=∠AHC,
∴∠AHC+∠AHF=∠FHB+∠AHF=180°,
∴C、H、F三点共线.
同理,E、K、F三点共线.
∴∠HDK=∠HDF+∠KDF=∠HFD+∠KFD=∠CFE,
又∵弧AC为30°,弧BE为70°,
∴弧CE为180°-30°-70°=80°,
∴∠CFE=
 ×80°=40°,
×80°=40°,∴∠HDK=40°.
故选B.
点评:本题主要考查了垂径定理,线段垂直平分线、等腰三角形的性质,圆周角定理及三点共线的证明方法.综合性强,有一定难度.

练习册系列答案
相关题目
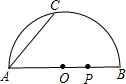 如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm.
如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm.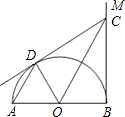 已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C.
已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C. 如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是
如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是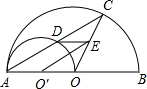 如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=