题目内容
 已知正比例函数和反比例函数的图象都经过点A(3,3).
已知正比例函数和反比例函数的图象都经过点A(3,3).
(1)求正比例函数和反比例函数的解析式;
(2)把直线OA向下平移后得到直线l,与反比例函数的图象交于点B(6,m),求m的值和直线l的解析式;
(3)在(2)中的直线l与x轴、y轴分别交于C、D,求四边形OABC的面积.
解:(1)设正比例函数的解析式为y=ax,反比例函数的解析式为y= ,
,
∵正比例函数和反比例函数的图象都经过点A(3,3),
∴3=3a,3= ,
,
∴a=1,b=9,
∴正比例函数的解析式为y=x,反比例函数的解析式为y= ;
;
(2)∵点B在反比例函数上,
∴m=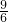 =
= ,
,
∴B点的坐标为(6, ),
),
∵直线BD是直线OA平移后所得的直线,
∴可设直线BD的解析式为y=x+c,
∴ =6+c,
=6+c,
∴c=- ,
,
 ∴直线l的解析式为y=x-
∴直线l的解析式为y=x- ;
;
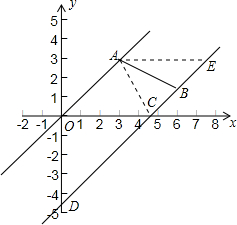
(3)过点A作AE∥x轴,交直线l于点E,连接AC.
∵直线l的解析式为y=x- ,A(3,3),
,A(3,3),
∴点E的坐标为( ,3),点C的坐标为(
,3),点C的坐标为( ,0).
,0).
∴AE= -3=
-3= ,OC=
,OC= ,
,
∴S四边形OABC=S△OAC+S△ACE-S△ABE
= ×
× ×3+
×3+ ×
× ×3-=
×3-= ×
× ×
×
=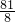 .
.
分析:(1)利用待定系数法,由正比例函数和反比例函数的图象都经过点A(3,3),即可求得解析式;
(2)由点B在反比例函数图象上,即可求得m的值;又由此一次函数是正比例函数平移得到的,可知一次函数与反比例函数的比例系数相同,代入点B的坐标即可求得解析式;
(3)构造直角梯形AEFD,则通过求解△ABE、△BDF与直角梯形ADFE的面积即可求得△ABD的面积.
点评:此题考查了反比例函数与一次函数的交点问题,待定系数法求函数的解析式,直线平移规律,四边形面积的求解方法等知识.主要考查学生数形结合的思想方法.
 ,
,∵正比例函数和反比例函数的图象都经过点A(3,3),
∴3=3a,3=
 ,
,∴a=1,b=9,
∴正比例函数的解析式为y=x,反比例函数的解析式为y=
 ;
;(2)∵点B在反比例函数上,
∴m=
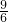 =
= ,
,∴B点的坐标为(6,
 ),
),∵直线BD是直线OA平移后所得的直线,
∴可设直线BD的解析式为y=x+c,
∴
 =6+c,
=6+c,∴c=-
 ,
, ∴直线l的解析式为y=x-
∴直线l的解析式为y=x- ;
;(3)过点A作AE∥x轴,交直线l于点E,连接AC.
∵直线l的解析式为y=x-
 ,A(3,3),
,A(3,3),∴点E的坐标为(
 ,3),点C的坐标为(
,3),点C的坐标为( ,0).
,0).∴AE=
 -3=
-3= ,OC=
,OC= ,
,∴S四边形OABC=S△OAC+S△ACE-S△ABE
=
 ×
× ×3+
×3+ ×
× ×3-=
×3-= ×
× ×
×
=
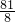 .
.分析:(1)利用待定系数法,由正比例函数和反比例函数的图象都经过点A(3,3),即可求得解析式;
(2)由点B在反比例函数图象上,即可求得m的值;又由此一次函数是正比例函数平移得到的,可知一次函数与反比例函数的比例系数相同,代入点B的坐标即可求得解析式;
(3)构造直角梯形AEFD,则通过求解△ABE、△BDF与直角梯形ADFE的面积即可求得△ABD的面积.
点评:此题考查了反比例函数与一次函数的交点问题,待定系数法求函数的解析式,直线平移规律,四边形面积的求解方法等知识.主要考查学生数形结合的思想方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 成正比例,y2与x2成反比.当x=1时,y=-12;当x=4时,y=7.
成正比例,y2与x2成反比.当x=1时,y=-12;当x=4时,y=7. 时,求y的值.
时,求y的值. 成正比例,y2与x2成反比.当x=1时,y=-12;当x=4时,y=7.
成正比例,y2与x2成反比.当x=1时,y=-12;当x=4时,y=7. 时,求y的值.
时,求y的值.