题目内容
【题目】如图，直线l过正方形ABCD的顶点B，点A、C至直线l的距离分别为2和3，则此正方形的面积为( )
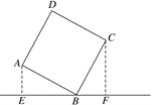
A. 5 B. 6 C. 9 D. 13
【答案】D
【解析】
由ABCD为正方形得到AB=BC，∠ABC为直角，再由AE与CF都垂直于EF，利用同角的余角相等得到一对角相等，再由一对直角相等，利用AAS得出△ABE与△BCF全等，由全等三角形对应边相等得到AE=BF，EB=CF，在直角三角形ABE中，利用勾股定理求出AB的长，即可确定出正方形的面积．
解：∵四边形ABCD为正方形，
∴AB=BC，∠ABC=90°，
∵AE⊥EF，CF⊥EF，
∴∠AEB=∠BFC=90°，
∴∠BAE+∠ABE=90°，∠ABE+∠CBF=90°，
∴∠BAE=∠CBF，
在△ABE和△BCF中，
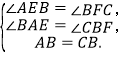
∴△ABE≌△BCF（AAS），
∴AE=BF=2，CF=EB=3，
根据勾股定理得：AB=
=
，
则正方形ABCD面积为13．
故选D.
【题目】新合作超市最近进了一批玩具，进价每个15元，今天共卖山20个，实际卖出的价格以每个18元为标准，超过的记为正，不足的记为负，记录如下：
实际每个售出价格与标准的差值（单位：元） | +3 | -1 | +2 | +1 |
个数 | 5 | 4 | 6 | 5 |
（1）这个超市今天卖出玩具的平均价格是多少？
（2）这个超市今天卖出的玩具赚了多少元？
【题目】
、
两仓库分别有水泥
吨和
吨，
、
两工地分别需要水泥
吨和
吨．已知从、仓库到、工地的运价如下表：
到 | 到 | |
| 每吨 | 每吨 |
| 每吨 | 每吨 |
1）若从仓库运到工地的水泥为
吨，则用含的代数式表示从仓库运到工地的水泥为_____吨，从仓库将水泥运到工地的运输费用为______元；
（2）求把全部水泥从、两仓库运到、两工地的总运输费（用含的代数式表示并化简）；
（3）如果从仓库运到工地的水泥为
吨时，那么总运输费为多少元？
