题目内容
已知:如图,AB是⊙O的一条弦,点C为 | AB |
(1)判定图中∠CEB与∠FDC的数量关系,并写出结论;
(2)将直线l绕C点旋转(与CD不重合),在旋转过程中,E点,F点的位置也随之变化,请你在下面两个备用图中分别画出在不同位置时,使(1)的结论仍然成立的图形,标上相应字母,选其中一个图形给予证明.
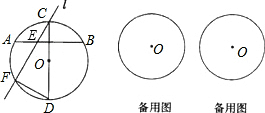
分析:根据垂径定理得到CD⊥AB,∠CFD=90°,然后通过等量代换求证出∠CEB=∠FDC.
解答: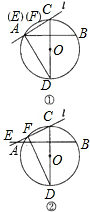 (1)解:∠CEB=∠FDC;
(1)解:∠CEB=∠FDC;
理由:∵CD是⊙O的直径,点C为
的中点,
∴CD⊥AB,
∴∠CEB+∠ECD=90°,
∵CD是⊙O的直径,
∴∠CFD=90°.
∴∠FDC+∠ECD=90°.
∴∠CEB=∠FDC.
(2)证明:如图②
∵CD是⊙O的直径,点C为
的中点,
∴CD⊥AB,
∴∠CEB+∠ECD=90°,
∵CD是⊙O的直径,
∴∠CFD=90°.
∴∠FDC+∠ECD=90°.
∴∠CEB=∠FDC.
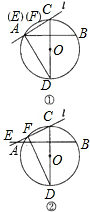 (1)解:∠CEB=∠FDC;
(1)解:∠CEB=∠FDC;理由:∵CD是⊙O的直径,点C为
 |
| AB |
∴CD⊥AB,
∴∠CEB+∠ECD=90°,
∵CD是⊙O的直径,
∴∠CFD=90°.
∴∠FDC+∠ECD=90°.
∴∠CEB=∠FDC.
(2)证明:如图②
∵CD是⊙O的直径,点C为
 |
| AB |
∴CD⊥AB,
∴∠CEB+∠ECD=90°,
∵CD是⊙O的直径,
∴∠CFD=90°.
∴∠FDC+∠ECD=90°.
∴∠CEB=∠FDC.
点评:本题考查垂径定理,这是需要熟练掌握的内容.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 22、已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.
22、已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC. (2013•门头沟区一模)已知:如图,AB是⊙O的直径,AC是⊙O的弦,M为AB上一点,过点M作DM⊥AB,交弦AC于点E,交⊙O于点F,且DC=DE.
(2013•门头沟区一模)已知:如图,AB是⊙O的直径,AC是⊙O的弦,M为AB上一点,过点M作DM⊥AB,交弦AC于点E,交⊙O于点F,且DC=DE. (1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.
(1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP. (2012•平谷区二模)已知,如图,AB是⊙O的直径,点E是
(2012•平谷区二模)已知,如图,AB是⊙O的直径,点E是 已知:如图,AB是⊙O的直径,BC为⊙O的切线,过点B的弦BD⊥OC交⊙O于点D,垂足为E.
已知:如图,AB是⊙O的直径,BC为⊙O的切线,过点B的弦BD⊥OC交⊙O于点D,垂足为E.