题目内容
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,tanC=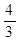 .求点D到BC边的距离.
.求点D到BC边的距离. 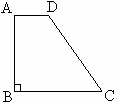
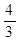 .求点D到BC边的距离.
.求点D到BC边的距离. 
解:作DE⊥BC于E,∵AD∥BC,∠B=90°
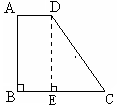 ∴四边形ABED是矩形,则AD=BE;
∴四边形ABED是矩形,则AD=BE;
∵AD=2,BC=5∴CE=BC-BE=BC-AD=3. 4分
∵tanC=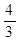 ,而tanC=
,而tanC=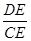 ,
,
∴DE=CE·tanC=3×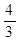 =4.
=4.
即点D到BC边的距离是4 8分
 ∴四边形ABED是矩形,则AD=BE;
∴四边形ABED是矩形,则AD=BE;∵AD=2,BC=5∴CE=BC-BE=BC-AD=3. 4分
∵tanC=
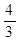 ,而tanC=
,而tanC=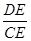 ,
,∴DE=CE·tanC=3×
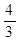 =4.
=4. 即点D到BC边的距离是4 8分
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
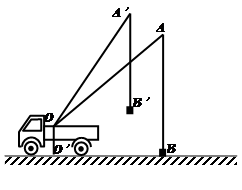
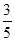 ,sinA′=
,sinA′=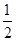 .
.
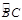 和弦AC的长. (弧长计算结果保留
和弦AC的长. (弧长计算结果保留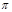 ,弦长精确到0.01)
,弦长精确到0.01)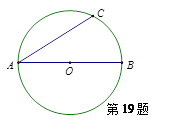

 ,求
,求 的长?
的长?

 ,则锐角α的度数是( )
,则锐角α的度数是( )