题目内容
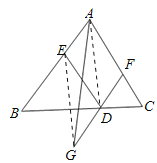
【题目】如图所示,已知D,E,F分别在△ABC的边BC,AB,AC上,且DE∥AF,DE=AF,将FD延长至G,使FG=2DF,连接AG,则ED,AG互相平分吗?请说明理由.
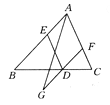
【答案】互相平分
【解析】试题分析:求ED与AG互相平分,只要证明四边形AEGD是平行四边形即可解答,由DE∥AC,DE=AF,可得四边形AEDF是平行四边形,所以,AE∥DF且AE=DF,又FG=2DF,则AE=GD,所以,四边形AEGD是平行四边形,即可得出ED与AG互相平分.
试题解析:证明:如图,连接AD,GE,∵DE∥AC,DE=AF,∴四边形AEDF是平行四边形,∴AE∥DF且AE=DF.又∵FG=2DF,∴AE=GD,∴四边形AEGD是平行四边形,∴ED与AG互相平分.

练习册系列答案
相关题目