题目内容
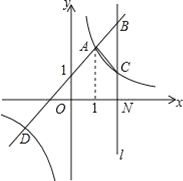
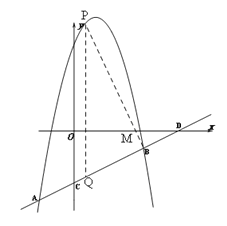
【题目】如图,直线![]() 与抛物线
与抛物线![]() 相交于A
相交于A![]() 和B(4,n)两点,点P是抛物线位于线段AB上方异于点A,B的一个动点,过点P作PQ⊥x轴,交线段AB于点Q.
和B(4,n)两点,点P是抛物线位于线段AB上方异于点A,B的一个动点,过点P作PQ⊥x轴,交线段AB于点Q.
(1)求抛物线的解析式;
(2)在P点运动过程中,线段PQ的长是否存在最大值?若存在,求出这个最大值,并求出此时P点的坐标;若不存在,请说明理由;
(3)直线AB与y轴交于点C,与x轴交于点D,若△PBQ与△ODC相似,求点P的坐标.

【答案】(1)![]() ;(2)线段PQ的长的最大值为9,此时P点坐标为(1,
;(2)线段PQ的长的最大值为9,此时P点坐标为(1, ![]() );(3)点P的坐标为(
);(3)点P的坐标为(![]() ,-1)或(
,-1)或(![]() ,6).
,6).
【解析】试题分析:(1)把A、B的坐标代入直线![]() ,即可得到m,n的值,从而得到A、B的坐标, 再把A、B的坐标代入抛物线的解析式,解方程即可得到结论;
,即可得到m,n的值,从而得到A、B的坐标, 再把A、B的坐标代入抛物线的解析式,解方程即可得到结论;
(2)设点P的横坐标为a,则P(a, ![]() ),Q(a,
),Q(a, ![]() ),用含a的代数式表示出PQ,配方即可得到结论;
),用含a的代数式表示出PQ,配方即可得到结论;
(3)分两种情况讨论:①当∠BPQ=90°时,②当∠PBQ=90°时.
试题解析:解:(1)∵A(m,-4)和B(4,n)在直线![]() 上,∴
上,∴![]() ,
, ![]() ,解得:m=-2,n=-1,∴A(-2,-4),B(4,-1), ∴
,解得:m=-2,n=-1,∴A(-2,-4),B(4,-1), ∴![]() ,解得:
,解得: 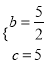 , ∴抛物线的解析式为
, ∴抛物线的解析式为![]() .
.
(2)设点P的横坐标为a,则P(a, ![]() ),Q(a,
),Q(a, ![]() ),
),
∴PQ=![]() ,∴当
,∴当![]() 时,线段PQ长取得最大值为9,此时P点坐标为(1,
时,线段PQ长取得最大值为9,此时P点坐标为(1, ![]() ).
).
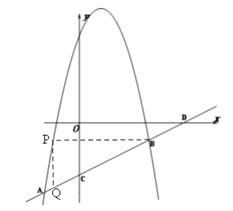
(3)∵PQ∥y轴,∴∠PQB=∠OCD.
∵∠COD=90°,∴当∠PBQ=90°或∠BPQ=90°时,△PBQ与△ODC相似.
①当∠BPQ=90°时,PB∥x轴,∴P点的纵坐标为-1,由![]() 得:
得: ![]() 或
或![]() ,∴P(
,∴P(![]() ,-1);
,-1);
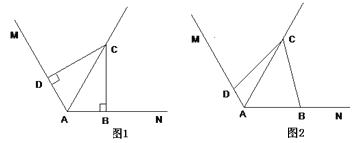
②当∠PBQ=90°时,设PB与x轴交于点M,由![]() 得:C(0,-3),D(6,0),∴OC=3,OD=6,∴CD=
得:C(0,-3),D(6,0),∴OC=3,OD=6,∴CD=![]() .
.
∵B(4,-1),∴BD=![]() .∵∠DBM=∠DOC=90°,∠BDM=∠ODC,∴△BDM∽△ODC,∴
.∵∠DBM=∠DOC=90°,∠BDM=∠ODC,∴△BDM∽△ODC,∴![]() ,即
,即![]() ,∴DM=
,∴DM=![]() ,∴OM=
,∴OM=![]() ,∴M(
,∴M(![]() ,0),∴直线PB的解析式为y=-2x+7.由
,0),∴直线PB的解析式为y=-2x+7.由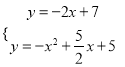 得:
得: ![]() ,
,  ,∴P(
,∴P(![]() ,6).
,6).
综上可知:点P的坐标为(![]() ,-1)或(
,-1)或(![]() ,6).
,6).

【题目】已知A、B在数轴上分别表示a,b.
(1)对照数轴填写下表:
a | 6 | -6 | -6 | -6 | 2 | -1.5 |
b | 4 | 0 | 4 | -4 | -10 | -1.5 |
A、B两点的距离 |
(2)若A、B两点间的距离记为d,试问:d和a,b有何数量关系?
(3)在数轴上标出所有符合条件的整数点P,使它到10和-10的距离之和为20,并求所有这些整数的和;
(4)找出(3)中满足到10和-10的距离之差大于1而小于5的整数的点P;
(5)若点C表示的数为x,当点C在什么位置时,![]() 取得的值最小?
取得的值最小?