题目内容
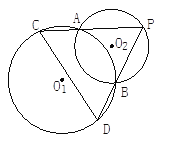
【题目】已知:如图,⊙O![]() 和⊙O
和⊙O![]() 相交于A、B两点, 动点P在⊙O
相交于A、B两点, 动点P在⊙O![]() 上,且在⊙
上,且在⊙![]() 外,直线PA、PB分别交⊙O
外,直线PA、PB分别交⊙O![]() 于C、D.问:⊙O
于C、D.问:⊙O![]() 的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明;
的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明;
【答案】CD的长与点P的位置无关.
【解析】试题分析:连接AD、AB,∠ADP在⊙O1中所对的弦为AB,所以∠ADP为定值,∠P在⊙O2中所对的弦为AB,所以∠P为定值.再利用三角形内角与外角的关系求出∠CAD为定值,则弦CD为定值,与P的位置无关.
试题解析:
当点P运动时,CD的长保持不变,A、B是⊙O1与⊙O2的交点,弦AB与点P的位置关系无关,
证明:
连接AD,如图所示:

∵∠ADP在⊙O1中所对的弦为AB,
∴∠ADP为定值,
∵∠P在⊙O2中所对的弦为AB,
∴∠P为定值,
∵∠CAD=∠ADP+∠P,
∴∠CAD为定值,
∵在⊙O1中∠CAD对弦CD,
∴CD的长与点P的位置无关.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目