题目内容
【题目】顺次连接任意四边形的各边中点得到的四边形一定是( )
A.正方形
B.矩形
C.菱形
D.平行四边形
【答案】D
【解析】解:连接BD, 已知任意四边形ABCD,E、F、G、H分别是各边中点.
在△ABD中,E、H是AB、AD中点,
所以EH∥BD,EH= ![]() BD.
BD.
在△BCD中,G、F是DC、BC中点,
所以GF∥BD,GF= ![]() BD,
BD,
所以EH=GF,EH∥DF,
所以四边形EFGH为平行四边形.
故选D.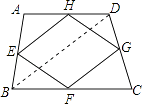
【考点精析】根据题目的已知条件,利用三角形中位线定理和平行四边形的判定的相关知识可以得到问题的答案,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.

练习册系列答案
相关题目
【题目】小聪是个数学爱好者,他发现从1开始,连续几个奇数相加,和的变化规律如右表所示:
加数个数 | 连续奇数的和S |
1 | 1= |
2 | 1+3=22 |
3 | 1+3+5=32 |
4 | 1+3+5+7=42 |
5 | 1+3+5+7+9=52 |
n | … |
(1)如果n=7,则S的值为;
(2)求1+3+5+7+…+199的值;
(3)求13+15+17+…+79的值.