题目内容
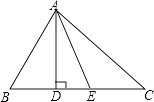
【题目】如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD上，则AP+PQ的最小值为（ ）
A．
B．
C．
D．
【答案】D．
【解析】
设BE=x，则DE=3x，∵四边形ABCD为矩形，且AE⊥BD，∴△ABE∽△DAE，∴
=BEDE，即
，∴AE=
x，在Rt△ADE中，由勾股定理可得
，即
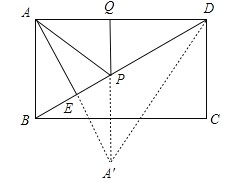
，解得x=，∴AE=3，DE=
，如图，设A点关于BD的对称点为A′，连接A′D，PA′，则A′A=2AE=6=AD，AD=A′D=6，∴△AA′D是等边三角形，∵PA=PA′，∴当A′、P、Q三点在一条线上时，A′P+PQ最小，又垂线段最短可知当PQ⊥AD时，A′P+PQ最小，∴AP+PQ=A′P+PQ=A′Q=DE=，故选D．
【题目】近年来，我市全面实行新型农村合作医疗，得到了广大农民的积极响应，很多农民看病贵、看病难的问题在合作医疗中得到了缓解．参加医保的农民可在规定的医院就医并按规定标准报销部分医疗费用，表①是医疗费用分段报销的标准；表②是甲、乙、丙三位农民今年的实际医疗费及个人承担总费用．
表①
医疗费用范围 | 门诊费 | 住院费（元） | ||
0～5000的部分 | 5001～20000的部分 | 20001及以上的部分 | ||
报销比例 | a% | 80% | 85% | c% |
表②
门诊费 | 住院费 | 个人承担总费用 | |
甲 | 260元 | 0元 | 182元 |
乙 | 80元 | 2800元 | b元 |
丙 | 400元 | 25000元 | 4030元 |
注明：
①个人承担医疗费=实际医疗费﹣按标准报销的金额；
②个人承担总费用包括门诊费和住院费中个人承担的部分．
③本题中费用精确到元．
请根据上述信息，解答下列问题：
（1）填空：a= ， b=；
（2）求住院费20001元及以上的部分报销医疗费用的比例c%；
（3）李大爷去年和今年的实际住院费共计52000元，他本人共承担了6850元，已知今年的住院费超过去年，则李大爷今年实际住院费用是多少元？