Question

【题目】如图所示的是由5个边长是1的正方形组成的图形．

（1）求BA12 ， BA22 ， BA32的值；
（2）从（1）中寻找规律，当有10个正方形时，求BA102的值；
（3）当有n个正方形时，求BAn2的值．

Answer 1

【答案】
（1）解：在Rt△ABA1中，BA12=AB2+A1A2=1+1=2，
在Rt△ABA2 ， 中，BA22=AB2+A2A2=1+22=5，
在Rt△ABA3 ， 中，BA32=AB2+A3A2=1+32=10
（2）解：∵2=1+12 ，
5=1+22 ，
10=1+32 ，
…
∴BA102=1+102=101
（3）解：根据上面的规律可知，BAn2=1+n2 ．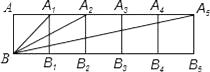

【解析】由边长是1的正方形，根据勾股定理求出BA12 ， BA22 ， BA32的值；（1）中寻找规律，得到2=1+12 ， 5=1+22 ， 10=1+32 ， ···，求出BA102的值；根据规律得到n个正方形时，求出BAn2的值．