Question

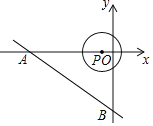
【题目】在直角坐标系中，已知直线分别于轴和轴交于,两点，将抛物线平移，得到抛物线，使抛物线过点,两点.

①求交点,的坐标；

②求抛物线的函数表达式；

③求抛物线的顶点坐标和对称轴方程.

Answer 1

【答案】①，；②；③顶点坐标，对称轴是直线.

【解析】

（1）利用坐标轴上点的坐标特点代入一次函数即可.

（2）根据抛物线平移a不变，设出C的解析式，再利用待定系数法求即可.

（3）利用顶点坐标公式和对称轴公式即可.

解：（1）∵直线分别于轴和轴交于,两点

将代入关系式解得：，故B点坐标为，

将代入关系式解得，故A点坐标为；

（2）∵抛物线平移得到抛物线，

∴可设抛物线的解析式为

∵抛物线过点,两点

∴将A、B两点坐标代入，得：

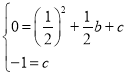
解得：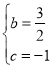

故抛物线C的解析式为：；

（3）将代入到顶点坐标公式（）可得顶点坐标为，对称轴为：直线.