题目内容
【题目】如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: ![]() ≈1.732)
≈1.732)
【答案】解:如图,过点C作CD⊥AB于点D,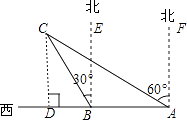
AB=20×1=20(海里),
∵∠CAF=60°,∠CBE=30°,
∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°﹣∠CAF=30°,
∴∠C=180°﹣∠CBA﹣∠CAB=30°,
∴∠C=∠CAB,
∴BC=BA=20(海里),
∠CBD=90°﹣∠CBE=60°,
∴CD=BCsin∠CBD= ![]() ≈17(海里).
≈17(海里).
【解析】过点C作CD⊥AB于点D,则若该船继续向西航行至离灯塔距离最近的位置为CD的长度,利用锐角三角函数关系进行求解即可.
【考点精析】利用锐角三角函数的定义对题目进行判断即可得到答案,需要熟知锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

练习册系列答案
相关题目
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?