题目内容
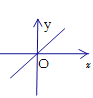
【题目】数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点A、B在数轴上分别对应的数为a、b,则A、B两点间的距离表示为|AB|=|a﹣b|.
![]()
根据以上知识解题:
(1)若数轴上两点A、B表示的数为x、﹣1,
①A、B之间的距离可用含x的式子表示为 ;
②若该两点之间的距离为2,那么x值为 .
(2)|x+1|+|x﹣2|的最小值为 ,此时x的取值是 ;
(3)已知(|x+1|+|x﹣2|)(|y﹣3|+|y+2|)=15,求x﹣2y的最大值 和最小值 .
【答案】(1)①|x+1|;②﹣3或1;(2)3,﹣1≤x≤2;(3)6,﹣7.
【解析】试题分析:(1)①根据题目已知中的 A、B 两点间的距离表示为|AB|=|a﹣b|.即可解答;②使①中的式子等于 2,解出即可;(2)求|x+1|+|x﹣2|的最小值,由线段的性质,两点之间,线段最短,可知当﹣1≤x≤2 时,|x+1|+|x﹣2|有最小值,再根据绝对值的性质即可求出最小值及x 的取值;(3)由于(|x+1|+|x﹣2|)(|y﹣3|+|y+2|)=15=3×5,可知﹣1≤x≤2,﹣2≤y≤3,依此得到 x﹣2y 的最大值和最小值.
试题解析:
(1)①A、B 之间的距离可用含 x 的式子表示为|x+1|;
②依题意有|x+1|=2,所以x+1=﹣2 或 x+1=2, 解得 x=﹣3 或 x=1.
(2)|x+1|+|x﹣2|的最小值为 3,此时 x 的取值是﹣1≤x≤2;
(3)∵(|x+1|+|x﹣2|)(|y﹣3|+|y+2|)=15,
∴﹣1≤x≤2,﹣2≤y≤3,
∴x﹣2y 的最大值为 2﹣2×(﹣2)=6,最小值为﹣1﹣2×3=﹣7.

【题目】小明骑自行车去学校,最初以某一速度匀速行驶,中途自行车发生故障,停下来修车耽误了几分钟,为了按时到校,他加快了速度,仍保持匀速行驶,结果准时到校,到校后,小明画了自行车行进路程s(km)与行进时间t(h)的图象,如图所示,请回答:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
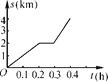
时间t/h | 0 | 0.2 | 0.3 | 0.4 |
路程s/km |
(3)路程s可以看成时间t的函数吗?