题目内容
由下列条件可以作出等腰三角形的是
- A.已知等腰三角形的两腰
- B.已知一腰和一腰上的高
- C.已知底角的度数和顶角的度数
- D.已知底边长和底边上的中线的长
D
分析:根据等腰三角形的性质(三线合一)以及线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等)可得已知底边长和底边上的中线的长可作出等腰三角形.
解答:已知等腰三角形的两腰,顶角不确定,不能作出等腰三角形,A错误;
已知一腰和一腰上的高,角度不确定,不能作出等腰三角形,B错误;
已知底角的度数和顶角的度数,只知道三个角,不能作出等腰三角形,C错误;
已知底边长和底边上的中线的长可作出等腰三角形,D正确.
故选D
点评:本题主要考查的是线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等)以及等腰三角形三线合一的定理可求解.
分析:根据等腰三角形的性质(三线合一)以及线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等)可得已知底边长和底边上的中线的长可作出等腰三角形.
解答:已知等腰三角形的两腰,顶角不确定,不能作出等腰三角形,A错误;
已知一腰和一腰上的高,角度不确定,不能作出等腰三角形,B错误;
已知底角的度数和顶角的度数,只知道三个角,不能作出等腰三角形,C错误;
已知底边长和底边上的中线的长可作出等腰三角形,D正确.
故选D
点评:本题主要考查的是线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等)以及等腰三角形三线合一的定理可求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




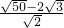 的值
的值 己如,△ABC的面积为1,分别延长AB、BC、CA到D、E、F,使AB=BD,BC=CE,CA=AF,连DE、EF、FD,则△DEF的面积为________.
己如,△ABC的面积为1,分别延长AB、BC、CA到D、E、F,使AB=BD,BC=CE,CA=AF,连DE、EF、FD,则△DEF的面积为________. 已知:如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为
已知:如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为



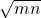 -2
-2 -4
-4 +4n=3,求
+4n=3,求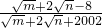 的值.
的值.