题目内容
正数m,n满足m+4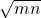 -2
-2 -4
-4 +4n=3,求
+4n=3,求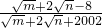 的值.
的值.
解:∵正数m,n满足m+4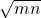 -2
-2 -4
-4 +4n=3,
+4n=3,
∴( +2
+2 )2-2(
)2-2( +2
+2 )-3=0,即(
)-3=0,即( +2
+2 -3)(
-3)( +2
+2 +1)=0,
+1)=0,
∴ +2
+2 =3或
=3或 +2
+2 =-1(不合题意,舍去),
=-1(不合题意,舍去),
∴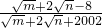 =
= =
= =
= ;即
;即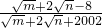 =
= .
.
分析:先利用完全平方公式化简左边,然后利用十字相乘法分解因式,并解方程求得 +2
+2 =3;最后将其代入所求的代数式求值即可.
=3;最后将其代入所求的代数式求值即可.
点评:本题考查了二次根式的化简求值.解答该题时,还可以采用换元法解答 +2
+2 的值.
的值.
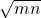 -2
-2 -4
-4 +4n=3,
+4n=3,∴(
 +2
+2 )2-2(
)2-2( +2
+2 )-3=0,即(
)-3=0,即( +2
+2 -3)(
-3)( +2
+2 +1)=0,
+1)=0,∴
 +2
+2 =3或
=3或 +2
+2 =-1(不合题意,舍去),
=-1(不合题意,舍去),∴
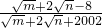 =
= =
= =
= ;即
;即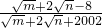 =
= .
.分析:先利用完全平方公式化简左边,然后利用十字相乘法分解因式,并解方程求得
 +2
+2 =3;最后将其代入所求的代数式求值即可.
=3;最后将其代入所求的代数式求值即可.点评:本题考查了二次根式的化简求值.解答该题时,还可以采用换元法解答
 +2
+2 的值.
的值. 
练习册系列答案
相关题目
一个分数的分子与分母都是正整数,且分子比分母小1,若分子和分母都减去1,则所得分数为小于
的正数,则满足上述条件的分数共有( )
| 6 |
| 7 |
| A、5个 | B、6个 | C、7个 | D、8个 |