题目内容
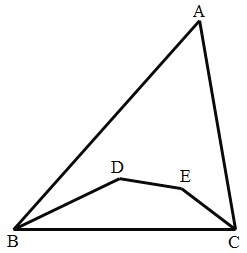
【题目】已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE

(1)如图1,当AE平分∠BAC时,EH⊥AB于H,△EHB的周长为10m,求AB的长;
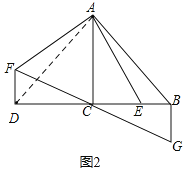
(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.
【答案】(1)AB=10m;(2)见解析.
【解析】
(1)根据等腰三角形的性质得到∠B=45°,根据角平分线的性质得到CE=EH=BH,根据全等三角形的性质得到AH=AC,于是得到结论;
(2)先连接AD,依据AAS判定△ADF≌△ABE,得到DF=BE,再判定△BCG≌△DCF,得出DF=BG,进而得到BG=BE.
解:(1)∵∠ACB=90°,AC=BC,
∴∠B=45°,
∵AE平分∠BAC时,EH⊥AB于H,
∴CE=EH=BH,
在Rt△ACE与Rt△AHE中,
![]() ,
,
∴Rt△ACE与Rt△AHE(HL),
∴AH=AC,
∴AH=BC,
∵△EHB的周长为10m,
∴AB=AH+BH=BC+BH=10m;
(2)如图所示,连接AD,
线段AE绕点A顺时针旋转90°得线段AF,则AE=AF,∠EAF=90°,
∵AC⊥BD,DC=BC,
∴AD=AB,∠ABE=∠ADC=45°,
∴∠BAD=90°=∠EAF,
∴∠BAE=∠DAF,
∴△ABE≌△ADF(SAS),
∴DF=BE,∠ADF=∠ABE=45°,
∴∠FDC=90°,
∵BG⊥BC,
∴∠CBG=∠CDF=90°,
又∵BC=DC,∠BCG=∠DCF,
∴△BCG≌△DCF(ASA),
∴DF=BG,
∴BG=BE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目