题目内容
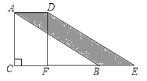
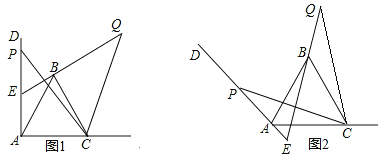
【题目】如图,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图,求∠QEP的度数;
(2)如图,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.
【答案】(1)60°,理由见解析;(2)BQ=2![]() ﹣2
﹣2![]() .
.
【解析】
(1)先证明出△CQB≌△CPA,即可得出∠QEP=60°;
(2)作CH⊥AD于H,如图2,证明△ACP≌△BCQ,则AP=BQ,由∠DAC=135°,∠ACP=15°,得出AH=3,CH=3![]() ,即可得出PH=CH=3
,即可得出PH=CH=3![]() ,即可得出结论.
,即可得出结论.
(1)如图1,∵PC=CQ,且∠PCQ=60°,则△CQB和△CPA中,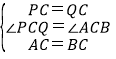 ,∴△CQB≌△CPA(SAS),
,∴△CQB≌△CPA(SAS),
∴∠CQB=∠CPA,又因为△PEM和△CQM中,∠EMP=∠CMQ, ∴∠QEP=∠QCP=60°.
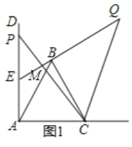
(2)作CH⊥AD于H,如图2,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵线段CP绕点C顺时针旋转60°得到线段CQ,
∴CP=CQ,∠PCQ=6O°,
∴∠ACB+∠BCP=∠BCP+∠PCQ,
即∠ACP=∠BCQ,
在△ACP和△BCQ中,
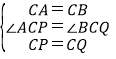
∴△ACP≌△BCQ(SAS),
∴AP=BQ,
∵∠DAC=135°,∠ACP=15°,∴∠APC=30°,∠PCB=45°,∴△ACH为等腰直角三角形,
∴AH=CH=![]() AC=
AC=![]() ×4=2
×4=2![]() ,在Rt△PHC中,PH=
,在Rt△PHC中,PH=![]() CH=2
CH=2![]() ,∴PA=PH﹣AH=2
,∴PA=PH﹣AH=2![]() ﹣2
﹣2![]() ,
,
∴BQ=2![]() ﹣2
﹣2![]() .
.


练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目